
DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000
Wiederholungstestat
Aufgaben und Lösungen
| Aufgabe | 1 | 2 | 3 | 4 | 5 | 6 | Summe | Note |
| erreichbare Punkte | 6 | 4 | 3 | 5 | 4 | 3 | 25 | |
| Ergebnis | | | | | | | | |
Es können insgesamt maximal 25 Punkte erreicht werden.
Zum Bestehen sind insgesamt mindestens 10 Punkte erforderlich.
Jede Lösung muß klar begründet werden.
Aufgabe 1.
a)
Formulieren Sie die Aussage
"Je zwei benachbarte Ecken liegen auf einem gemeinsamen (graphentheoretischen) Kreis der
Länge 3" in der Sprache erster Ordnung mit technischen Zeichen
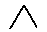 ,
, 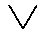 ,
,
 ,
,  ,
,
 ,
, 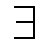 , (, ), = ,
und mit Symbolmenge {a,b,c,..., R},
wobei R für eine binäre Relation (für die Adjazenzrelation) steht.
, (, ), = ,
und mit Symbolmenge {a,b,c,..., R},
wobei R für eine binäre Relation (für die Adjazenzrelation) steht.
b)
Prüfen Sie, welcher der 4 gegebenen Graphen ein Modell für diese
Formel ist.
- V = {1,2,3,4,5}, E = {{1,2},{2,3},{1,3},{1,4},{4,5},{1,5}},
- V = {1,2,3,4}, E = {{1,2},{1,3},{2,3},{2,4},{3,4}},
- V = {1}, E = Ø,
- V = {1,2,3,4,5,6}, E = {{1,2},{1,5},{2,4},{2,5},{3,4},{3,5}, { 3,6},{4,6}}.
c)
Bringen Sie die Formel in pränexe konjunktive Normalform.
Lösung:
a)  x
x  y
(R x y
y
(R x y 
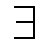 z
(R x z
z
(R x z 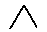 R y z)).
R y z)).
b) Der erste(1 und 2 liegen im 3-Kreis 1,2,3;
ebenso 2 und 3 sowie 1 und 3.
1 und 4 liegen im 3-Kreis 1,4,5; ebenso 1 und 4 sowie
4 und 5), zweite(genauso ...),
und dritte Graph(für benachbarte Ecken gilt hier ALLES,
da es keine benachbarten Ecken gibt) ist ein
Modell,
der vierte Graph nicht(denn 3 und 4 liegen in keinem 3-Kreis)
c) Wir formen
äquivalent um, indem wir
zuerst die Implikation ersetzen, dann eine der Äquivalenzen der
Liste benutzen
(z kommt in  R x y nicht frei vor),
und schließlich ein
Distributivgesetz anwenden:
R x y nicht frei vor),
und schließlich ein
Distributivgesetz anwenden:
 x
x  y
(
y
( R x y
R x y 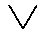
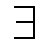 z (R x z
z (R x z 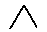 R y z))
R y z))
 x
x  y
y
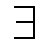 z (
z ( R x y
R x y 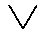 (R x z
(R x z 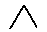 R y z))
R y z))
 x
x
 y
y 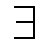 z
((
z
(( R x y
R x y 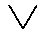 R x z)
R x z)
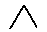 (
( R x y
R x y 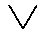 R y z))
R y z))
Aufgabe 2.
Die Abbildung
f: P({1,2,3})  N0 sei durch
f(S) =
N0 sei durch
f(S) = 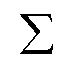 x
x  S x gegeben, wobei f(Ø) = 0
gesetzt wird.
Wir definieren eine Relation auf P({1,2,3}) durch
(S,T)
S x gegeben, wobei f(Ø) = 0
gesetzt wird.
Wir definieren eine Relation auf P({1,2,3}) durch
(S,T)  R falls f(S)
R falls f(S)
 f(T) ist.
f(T) ist.
a) Stellen Sie die Relationen R und R ° R als 0,1-Matrizen dar.
b) Ist R eine Ordnungsrelation (mit Begründung!)?
Zur Erinnerung: Für eine Menge M bezeichnet P(M) die Potenzmenge von M,
d.h. die Menge aller Teilmengen von M.
Lösung:
R und
R ° R
haben dieselbe Matrix, nämlich
|
Ø |
{ 1 } |
{ 2 } |
{ 3 } |
{ 1,2 } |
{ 1,3 } |
{ 2,3 } |
{ 1,2,3 } |
| Ø |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| { 1 } |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| { 2 } |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
| { 3 } |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
| { 1,2 } |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
2
| { 1,3 } |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
| { 2,3 } |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
| { 1,2,3 } | 0 |
0 | 0 |
0 | 0 |
0 | 0 |
1 |
Das ist "fast" die Matrix einer linear geordneten Menge,
aber eben nicht ganz-die "1" an der Stelle 5,4 stört.
Weil also ({ 1,2 },{ 3 })  R und
({3},{1,2})
R und
({3},{1,2})  R gilt, ohne daß
{1,2} = {3} gilt, ist die Antisymmetrie verletzt,
weshalb R keine
Ordnungsrelation ist.
R gilt, ohne daß
{1,2} = {3} gilt, ist die Antisymmetrie verletzt,
weshalb R keine
Ordnungsrelation ist.
Aufgabe 3.
Im Grundstudium werden 8 verschiedene Vorlesungen
G1, G2, ... , G8,
und im Hauptstudium 9 verschiedene Vorlesungen
H1, H2, ... ,
H9 angeboten. Der Studienplan sieht vor,
daß von den Grundstudiumsvorleungen genau 5 Scheine erzielt werden
müssen, während von den Hauptstudiumsvorlesungen mindestens 7
Scheine erzielt werden müssen. Wieviel zulässige Scheinkombinationen gibt
es, wobei die Reihenfolge der Scheine irrelevant ist?
Begründen Sie die Formel ausführlich!
Formeller ausgedrückt: Wieviel Teilmengen M der Menge
{G1, G2, ... ,
G8, H1, H2, ... ,
H9 } erfüllen
|M  {G1, G2, ... ,
G8}| = 5
und |M
{G1, G2, ... ,
G8}| = 5
und |M  {H1, H2, ... ,
H9}|
{H1, H2, ... ,
H9}| 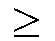 7?
7?
Lösung:
Im Grundstudium wählt man 5 aus 8 Vorlesungen, dafür gibt
es
(8 über 5)
= 8*7*6/(3*2*1) = 56 Möglichkeiten.
Im Hauptstudium gibt es 3 Typen: "Streber",
Ïnteressierte", und
"DienstnachVorschriftler", die jeweils 9, 8, bzw. 7 Vorlesungen
besuchen. Da jeder erfolgreiche Student genau einem dieser Typen
zuzuordnen ist, und die Scheinmöglichkeiten für
Streber, Interessierte, und DienstnachVorschriftler
jeweils (9 über 9)=1, (9 über 8) = 9, bzw. (9 über 7) =
9*8/(2*1) = 36 sind, ergeben sich mit der
Summenregel
insgesamt 1 + 9 + 36 = 46 Möglichkeiten fürs Hauptstudium.
Da die Wahlen im Grund- und Hauptstudium unabhängig sind, gibt es,
mit der
Produktregel,
insgesamt 56*46 = (50+6)*(50-4) =
2500 + 100 - 24 = 2576 Möglichkeiten für
ein erfolgreiches Studium.
Aufgabe 4.
T sei die Menge aller transitiven Relationen auf der Menge {a,b,c,d,e}.
a) Welche der folgenden Relationen sind Elemente von T?
R1 = {(a,b),(b,c),(a,c)},
R2 = {(a,b),(a,d),(b,a),(b,d),(d,a),(d,b)},
R3 = {(b,c),(b,d),(c,d)}.
b) Es ist bekannt, daß T bezüglich der
Teilmengenrelation  ein Verband ist.
Bilden Sie für alle Paare (i,j) mit 1
ein Verband ist.
Bilden Sie für alle Paare (i,j) mit 1  i < j
i < j  3,
für die Ri und Rj Elemente von T sind,
das Supremum (kleinste obere Schranke) sup(Ri,Rj) und das Infimum
(größ te untere Schranke) inf(Ri,Rj)
im Verband (T,
3,
für die Ri und Rj Elemente von T sind,
das Supremum (kleinste obere Schranke) sup(Ri,Rj) und das Infimum
(größ te untere Schranke) inf(Ri,Rj)
im Verband (T,  ).
).
Lösung:
a)
R1 und R3 sind
transitiv, R2 aber nicht,
denn da (a,b)  R2 und (b,a)
R2 und (b,a)
 R2 gilt, müsste
auch (a,a)
R2 gilt, müsste
auch (a,a)  R2 folgen,
was aber nicht gilt.
R2 folgen,
was aber nicht gilt.
b) Es ist auch bekannt, daß hier das
Supremum die
transitive Hülle
der Vereinigung ist, und das
Infimum der Durchschnitt
der Relationen.
Wir haben R1  R3
= { (a,b), (a,c), (b,c), (b,d), (c,d) }.
Die transitive Hülle davon ist
sup(R1,R2) = (R1
R3
= { (a,b), (a,c), (b,c), (b,d), (c,d) }.
Die transitive Hülle davon ist
sup(R1,R2) = (R1
 R3)* = { (a,b), (a,c), (a,d), (b,c), (b,d), (c,d) }.
Dagegen ist inf(R1,R2) =
(R1
R3)* = { (a,b), (a,c), (a,d), (b,c), (b,d), (c,d) }.
Dagegen ist inf(R1,R2) =
(R1  R3) = { (b,c) }.
R3) = { (b,c) }.
Aufgabe 5.
Lösen Sie
die Rekursionsgleichung:
|
an = 2 an - 1
+ 3 an - 2,
n ...
3, |
|
mit Anfangswerten a1 = 2 und a2 = 4.
Lösung (
siehe hier):
Wir schreiben die Gleichung um in
am+2 - 2 am+1 - 3 am
und erhalten die charakteristische Gleichung
x2 - 2x - 3
= 0 mit den Nullstellen
x1 = 1 + 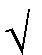 (1+3) = 3 und
x2 = 1 -
(1+3) = 3 und
x2 = 1 -
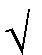 (1+3) = - 1.
Also hat die Lösung die Form
an = B*3n + C*(-
1)n.
2
(1+3) = - 1.
Also hat die Lösung die Form
an = B*3n + C*(-
1)n.
2
Die Anfangswerte mit n = 1 und n = 2 ergeben die beiden Gleichungen
2 = a1 = B*31 + C*(- 1)1 = 3*B - C
und 4 = a2 = B*32 + C*(- 1)
2 = 9*B + C.
Dieses Gleichungssystem hat die Lösung
B = 1/2 und C = -1/2.
Die Lösung ist also
an = 0.5*3n -
0.5*(- 1)n
Aufgabe 6.
Welche der Formeln B oder  B
ist aus den 5 gegebenen Formeln
B
ist aus den 5 gegebenen Formeln
 D, C
D, C  A,
A,
 C
C  B,
A
B,
A 
 B,
A
B,
A  D ableitbar?
Leiten Sie die ableitbare Formel nur unter Benutzung folgender 3
Schlussregeln ab:
D ableitbar?
Leiten Sie die ableitbare Formel nur unter Benutzung folgender 3
Schlussregeln ab:
Geben Sie bei jedem Ableitungsschritt die verwendete Regel an.
Lösung:
| (1) |
 D D |
|
| (2) |
C  A A |
|
| (3) |
 C C  B B |
|
| (4) |
A   B B |
|
| (5) |
A  D D |
|
| (6) |
 A A |
(Modus Tollens mit (1) und (5)) |
| (7) |
 C C |
(Modus Tollens mit (6) und (2)) |
| (8) |
B |
(Modus Ponens mit (3) und (7)) |
Erich Prisner
File translated from TEX by TTH, version 2.53.
On 14 Jul 2000, 17:29.
