2.1
Mister X will am 19.04.00 von Cottbus über Leipzig nach Frankfurt(Main)
fahren.
Die Abfahrt in Cottbus soll zwischen 05.00 und 09.00 Uhr
liegen.
Die Wartezeit in Leipzig (d.h. die Zeit zwischen der
fahrplanmäßigen Ankunft und Abfahrt)
soll 10 bis 60 Minuten betragen.
Der Zugfahrplan
der direkten
Züge zwischen von Cottbus und Leipzig bzw. zwischen Leipzig und
Frankfurt sei bekannt (
http://bahn.hafas.de/bin/db.s98/query.exe/dn).
Wie erhält man die entsprechenden Ankunftszeiten in
Frankfurt?
Gefordert ist nicht nur die Angabe der richtigen Zeiten, sondern eine
Formulierung der Aufgabe durch (drei) Relationen (auf der Menge aller
Zeitpunkte).
2.2 Wir ordnen die Menge M aller endlichen oder unendlichen 0-1 Worte, durch a £ b falls a endliches Anfangswort von b ist. Finden Sie alle maximalen Elemente, begründen Sie, daß jedes nichtmaximale Element einen (unmittelbaren) oberen Nachbarn hat, und zeigen Sie, daß es nichtminimale Elemente gibt, die keinen (unmittelbaren) unteren Nachbarn haben.
2.3
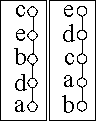
Es seien zwei lineare Ordnungen L1, L2,
auf {a,b,c,d,e} gegeben, siehe die Hasse Diagramme rechts.
Zeigen Sie, daß der Durchschnitt der Relationen
L1Ç L2
wieder eine Ordnungsrelation ist, und zeichnen Sie das Hasse Diagramm.
b) Ist der Durchschnitt zweier Ordnungsrelationen immer wieder
Ordnungsrelation?
2.4 (optional) Die Teilbarkeitsrelation "|" ist auf der Menge N der natürlichen Zahlen eine Ordnungsrelation. Gibt es in (N, | ) zu jeder Menge ein Supremum oder zu jeder Menge ein Infimum?