DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000

Eine Relation f A × B ist eine Abbildung f: A B von A in B, falls es zu jedem a A genau ein b B mit (a,b) f gibt. Wir schreiben dann b = f(a). In der Analysis haben wir oft mit partiellen Abbildungen f: A B zu tun --- Relationen, bei denen es zu jedem a A höchstens ein b B mit (a,b) f. Die Menge der a A für die es so ein f(a) gibt, wird der Definitionsbereich genannt.

Eine Abbildung f: A B ist injektiv falls es zu jedem b B höchstens eine a A mit (a,b) f (d.h. f(a)=b) gibt, d.h. falls aus f(a1) = f(a2) stets a1 = a2 folgt, surjektiv falls es zu jedem b B mindestens eine a A mit f(a)=b gibt, bijektiv, wenn sie injektiv und surjektiv ist.

Definition: Für jede Abbildung f: A B und Teilmengen A' A, B' B definieren wir f(A') = {f(a)| a A'} f-1 (B') = {a A| f(a) B'}

Für jede Abbildung f: A B ist A' f-1 (f(A')), f(f-1 (B')) B'. f(A1 A2) f(A1) f(A2), f(A1 A2) = f(A1) f(A2), f-1(B1 B2) = f- 1(B1) f -1(B2), f-1(B1 B2) = f-1 (B1) f -1(B2),

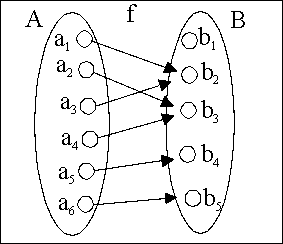
Haben wir zwei Abbildungen f: A B und g: C D, so kann man die Komposition g ° f: A D mit (g°f)(x) = g(f(x)) bilden falls f(A) C ist.
Unter obigen Voraussetzungen ist g ° f injektiv, falls f und g beide injektiv sind. Falls g surjektiv ist und f(A)=C ist (also insbesondere falls f und g surjektiv sind und B=C ist) ist g ° f surjektiv.
Umgekehrt folgt aus der Injektivität von g ° f die Injektivität von f, und aus der Surjektivität von g ° f die Surjektivität von g.

Falls f: A B bijektiv ist, gibt es eine Abbildung f^-1: B A die mit der Eigenschaft f(f^-1(b)) = b und f^-1(f(a))=a für alle a A und alle b B. Diese Abbildung wird die Umkehrabbildung von f genannt.