
DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000
Binäre Relationen
auf einer Menge
Inhalt:
Binäre Relationen R  A ×A
auf einer Menge A
werden manchmal auch homogene
(binäre) Relationen genannt. Die (Nicht-) Gültigkeit einiger
Eigenschaften entscheidet, ob die Relation
Ordnungsrelation,
Äquivalenzrelation, oder ein
(ungerichteter) Graph ist.
Wir werden zwei Möglichkeiten solche Relationen darzustellen
kennenlernen---einerseits durch quadratische 0-1 Matrizen, andererseits
als gerichtete Graphen.
A ×A
auf einer Menge A
werden manchmal auch homogene
(binäre) Relationen genannt. Die (Nicht-) Gültigkeit einiger
Eigenschaften entscheidet, ob die Relation
Ordnungsrelation,
Äquivalenzrelation, oder ein
(ungerichteter) Graph ist.
Wir werden zwei Möglichkeiten solche Relationen darzustellen
kennenlernen---einerseits durch quadratische 0-1 Matrizen, andererseits
als gerichtete Graphen.
Relationen auf einer festen Menge A kann man schneiden und vereinigen, und man
kann auch das Komplement bilden. Ausserdem kann man Transponieren,
und Komponieren; tatsächlich hat die Menge aller Relationen
auf A einige interessante Eigenschaften bzgl. dieser Operationen.
Definition:
Eine binäre Relation R  A ×A
auf A heißt A ×A
auf A heißt
- reflexiv falls (a,a)
 R
für jedes a R
für jedes a  A gilt. A gilt.
- irreflexiv falls für kein a
 A
gilt (a,a) A
gilt (a,a)  R. R.
- symmetrisch falls aus (a,b)
 R
immer auch (b,a) R
immer auch (b,a)  R folgt. R folgt.
- antisymmetrisch falls aus
(a,b), (b,a)
 R folgt a= b. R folgt a= b.
- transitiv falls aus (a,b)
 R und
(b,c) R und
(b,c)  R immer auch
(a,c) R immer auch
(a,c)  R folgt. R folgt.
|
Die natürlichste binäre Relation auf einer Menge A
ist die Identität
(oder Gleichheitsrelation, Diagonale)
idA = {(a,a) | a  A}.
A}.
Darstellung binärer Relationen
Binäre Relationen auf endlichen Mengen M
können auf zwei Arten visualiert werden.
Erstens durch quadratische |M| × |M| 0-1 Matrizen.
Zuerst muß man die Elemente von M als
x1,x2,...,x|M|
durchnummerieren. Für i,j  {1,2,..|M|}
definiert man ai,j = 1
falls (xi,xj)
{1,2,..|M|}
definiert man ai,j = 1
falls (xi,xj)  R,
und andernfalls ai,j = 0.
R,
und andernfalls ai,j = 0.
Die zweite
Visualisierungsmöglichkeit benutzt sogenannte
gerichtete Graphen oder (Digraphen).
Die Elemente von M werden aufs Blatt
gezeichnet und Ecken genannt.
Nun zieht man einen Pfeil (gerichtete Kante)
von x nach y wenn
(x,y)  R ist. Eventuelle
gerichtete Kanten von x nach x werden wegen ihrer Bumerangnatur
Schlingen genannt.
Natürlich kann dieselbe Relation, d.h. derselbe Digraph
sehr verschieden gezeichnet werden.
R ist. Eventuelle
gerichtete Kanten von x nach x werden wegen ihrer Bumerangnatur
Schlingen genannt.
Natürlich kann dieselbe Relation, d.h. derselbe Digraph
sehr verschieden gezeichnet werden.
|
Beispiel:
Sei M = {a,b,c,d,e} und R={(a,b),(a,e),(b,a),(b,d),(c,d),(e,e)}.
Hier ist die Matrix (für Reihenfolge a,b,c,d,e)
und der gerichtete Graph.
|
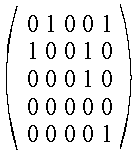 |
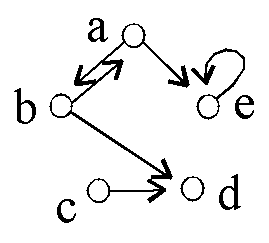 |
Homomorphismen/Isomorphie
Wie bei jeder mathematischen Struktur gibt es auch
hier den Begriff des Homomorphismus und der Isomorphie.
Ein Homomorphismus
von einer Relation
R  A ×A
auf eine Relation
R'
A ×A
auf eine Relation
R'  A' ×A'
ist eine Abbildung f: A
A' ×A'
ist eine Abbildung f: A  A'
mit der Eigenschaft daß aus
(x,y)
A'
mit der Eigenschaft daß aus
(x,y)  R
stets (f(x),f(y))
R
stets (f(x),f(y))  R' folgt.
R' folgt.
Zwei Relationen R  A ×A
und R'
A ×A
und R'  A' ×A' sind
isomorph
wenn es eine bijektive Abbildung f: A
A' ×A' sind
isomorph
wenn es eine bijektive Abbildung f: A  A'
gibt, so daß sowohl f als auch f-1
Homomorphismen sind.
Isomorphe binäre Relationen sind bis auf
Benennung der Elemente dieselben Strukturen.
A'
gibt, so daß sowohl f als auch f-1
Homomorphismen sind.
Isomorphe binäre Relationen sind bis auf
Benennung der Elemente dieselben Strukturen.
Aus gegebenen Relationen lassen sich neue bilden.
Einerseits durch Durchschnitts-, Vereinigungs- und Komplementsbildung
(wir setzen  R := (A ×A) \ R),
denn Relationen sind ja Mengen,
andererseits auch durch folgende Operationen:
R := (A ×A) \ R),
denn Relationen sind ja Mengen,
andererseits auch durch folgende Operationen:
Die Transposition oder inverse Relation RT
zu einer Relation R auf A ist definiert als
RT = {(b,a) | (a,b)  R}.
Ist R eine Abbildung, so ist RT = R-1.
Die Bezeichnung rührt daher, daß die Matrix von RT
gleich der transponierten Matrix von R ist. Den gerichteten Graphen
von RT erhält man durch Umdrehen aller Richtungen.
R}.
Ist R eine Abbildung, so ist RT = R-1.
Die Bezeichnung rührt daher, daß die Matrix von RT
gleich der transponierten Matrix von R ist. Den gerichteten Graphen
von RT erhält man durch Umdrehen aller Richtungen.
Sind R und S Relationen auf einer Menge A,
so ist die Komposition (das Relationenprodukt)
R ° S = {(a,c) | 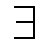 b
b  A:
(a,b)
A:
(a,b)  R
R 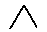 (b,c)
(b,c)  S}. Dummerweise ist die Konvention genau
umgekehrt wie bei Abbildungen: Sind f und g Abbildungen, so ist
f ° g (als Relationenprodukt) = g ° f (als Komposition von Abbildungen),
also aufpassen!
S}. Dummerweise ist die Konvention genau
umgekehrt wie bei Abbildungen: Sind f und g Abbildungen, so ist
f ° g (als Relationenprodukt) = g ° f (als Komposition von Abbildungen),
also aufpassen!
Die Matrix von R ° S ist das Matrizenprodukt der Matrizen von R und S,
wenn man beim Addieren "1 + 1 = 1" beachtet
(man möchte ja wieder eine 0-1 Matrix erhalten---andernfalls
würde man die Zahl der b  A
mit (a,b)
A
mit (a,b)  R und (b,c)
R und (b,c)  R
zählen).
Man kann R ° S auch aus der Digraphendarstellung ablesen:
Färbt man alle gerichtete Kanten von R rot
und alle gerichtete Kanten von S schwarz,
dann ist ganu dann (x,y)
R
zählen).
Man kann R ° S auch aus der Digraphendarstellung ablesen:
Färbt man alle gerichtete Kanten von R rot
und alle gerichtete Kanten von S schwarz,
dann ist ganu dann (x,y)  R ° S falls man durch
einen "Doppelzug", erst entlang einer roten Kante,
danach entlang einer schwarzen Kante,
von x nach y kommen kann.
R ° S falls man durch
einen "Doppelzug", erst entlang einer roten Kante,
danach entlang einer schwarzen Kante,
von x nach y kommen kann.
R ist genau dann
- reflexiv, wenn idA
 R,
R,
- irreflexiv, falls idA
 R =
R =
 ,
,
- symmetrisch, falls R = RT,
- antisymmetrisch, wenn R
 RT
RT
 idA,
idA,
- transitiv, falls R ° R
 R.
R.
Relationenalgebra
Wir betrachten die Menge aller Relationen auf einer festen Menge A.
Mit den drei ausgezeichneten Relationen
 , idA, sowie
1A := A ×A erhalten wir:
, idA, sowie
1A := A ×A erhalten wir:
- (RT)T = R,
- (
 R)T =
R)T =  (RT),
(RT),
- idAT = idA,
 T =
T =  ,
1AT = 1A,
,
1AT = 1A,
- (Q ° R) ° S = Q ° (R ° S) (Assoziativgesetz),
- idA ° R = R ° idA = R,
- 1A ° R ° 1A = 1A
für jedes R
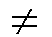
 ("Tarski-Regel"),
("Tarski-Regel"),
- (R ° S)T = ST ° RT (vgl. Lin.Algebra),
- Q ° R
 S genau dann wenn
QT °
S genau dann wenn
QT °  S
S 
 R genau dann wenn
R genau dann wenn
 S ° RT
S ° RT

 Q ("Schröder-Umformung")
Beweis,
Beispiel
Q ("Schröder-Umformung")
Beweis,
Beispiel
- (Q ° R)
 S
S  (Q
(Q  (S ° RT)) °
(R
(S ° RT)) °
(R  (QT ° S)) ("Dedekind-Formel"),
Beweis
(QT ° S)) ("Dedekind-Formel"),
Beweis
- R °
 =
=  ° R =
° R =  ,
,
- Wenn P
 Q und R
Q und R  S,
dann P ° R
S,
dann P ° R  Q ° S,
Q ° S,
- Q ° (R
 S) =
(Q ° R)
S) =
(Q ° R)  (Q ° S) und
Q ° (R
(Q ° S) und
Q ° (R  S) = (Q ° R)
S) = (Q ° R)  (Q ° S)
(Distributivgesetze mit °).
(Q ° S)
(Distributivgesetze mit °).
Hüllen
Für jede Relation R  A ×A
ist R
A ×A
ist R  idA reflexiv und
R
idA reflexiv und
R  RT symmetrisch. Die
Relationen sind die kleinsten reflexiven bzw. symmetrischen Relationen auf A,
die R enthalten. Ähnliches ist auch für "transitiv" möglich:
RT symmetrisch. Die
Relationen sind die kleinsten reflexiven bzw. symmetrischen Relationen auf A,
die R enthalten. Ähnliches ist auch für "transitiv" möglich:
Die transitive Hülle R*
einer binären Relation R auf einer Menge M
wird definiert durch:
(x,y)  R*
Û R*
Û 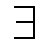 k k
 N0: N0: 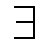 z1, z2, ... , zk
z1, z2, ... , zk
 M: (x,z1),
(z1,z2),
... , (zk-
1,zk),
(zk,y) M: (x,z1),
(z1,z2),
... , (zk-
1,zk),
(zk,y)  R. R.
|
Definiert man R0 = idM
und Rn+1 = Rn ° R,
dann kann man die transitive Hülle auch so ausdrücken:
R* = 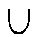 n
n 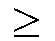 0 Rn.
Der Name ist gerechtfertigt, denn sind (x,y), (y,w)
0 Rn.
Der Name ist gerechtfertigt, denn sind (x,y), (y,w)
 R*, d.h.
gibt es natürliche Zahlen k, t
R*, d.h.
gibt es natürliche Zahlen k, t 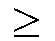 0
und
z1, z2, ... , zk,
u1, u2, ... , ut
0
und
z1, z2, ... , zk,
u1, u2, ... , ut
 M: mit (x,z1),
(z1,z2),
... , (zk-
1,zk),
(zk,y)
M: mit (x,z1),
(z1,z2),
... , (zk-
1,zk),
(zk,y)  R,
und (y,u1),
(u1,u2),
... , (ut-
1,ut)
R,
und (y,u1),
(u1,u2),
... , (ut-
1,ut)  R,
(ut,w), so ist ja offenbar damit auch
(x,w)
R,
(ut,w), so ist ja offenbar damit auch
(x,w)  R*
R*
 Die transitive Hülle jeder binären Relation auf einer Menge
ist transitiv.
Die transitive Hülle jeder binären Relation auf einer Menge
ist transitiv.
Test
Gegeben sind 6 binäre Relationen auf {a,b,c,d,e}:
D1: D2:
D2: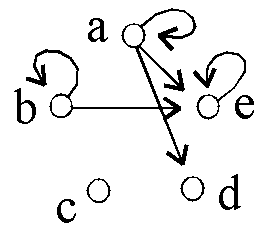 D3:
D3: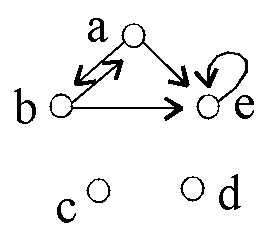
D4: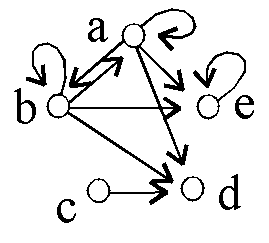 D5:
D5: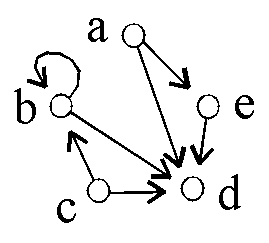 D6:
D6: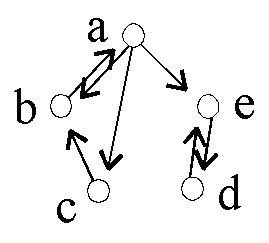
|
D1* = ? |
|
|
Was ist D1 ° D1? |
|
|
irreflexiv ist ... |
|
|
transitiv ist ... |
|
|

|
Die wichtigsten biären Relationen auf einer Menge sind
Ordnungsrelationen,
Äquivalenzrelationen und
(ungerichtete) Graphen.
Erich Prisner
erstellt im Februar 2000, zuletzt geändert am 11. April 2000.

![]() A}.
A}.
![]() {1,2,..|M|}
definiert man ai,j = 1
falls (xi,xj)
{1,2,..|M|}
definiert man ai,j = 1
falls (xi,xj) ![]() R,
und andernfalls ai,j = 0.
R,
und andernfalls ai,j = 0.
![]() R ist. Eventuelle
gerichtete Kanten von x nach x werden wegen ihrer Bumerangnatur
Schlingen genannt.
Natürlich kann dieselbe Relation, d.h. derselbe Digraph
sehr verschieden gezeichnet werden.
R ist. Eventuelle
gerichtete Kanten von x nach x werden wegen ihrer Bumerangnatur
Schlingen genannt.
Natürlich kann dieselbe Relation, d.h. derselbe Digraph
sehr verschieden gezeichnet werden.
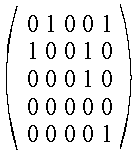

![]() A ×A
und R'
A ×A
und R' ![]() A' ×A' sind
isomorph
wenn es eine bijektive Abbildung f: A
A' ×A' sind
isomorph
wenn es eine bijektive Abbildung f: A ![]() A'
gibt, so daß sowohl f als auch f-1
Homomorphismen sind.
Isomorphe binäre Relationen sind bis auf
Benennung der Elemente dieselben Strukturen.
A'
gibt, so daß sowohl f als auch f-1
Homomorphismen sind.
Isomorphe binäre Relationen sind bis auf
Benennung der Elemente dieselben Strukturen.
![]() R}.
Ist R eine Abbildung, so ist RT = R-1.
Die Bezeichnung rührt daher, daß die Matrix von RT
gleich der transponierten Matrix von R ist. Den gerichteten Graphen
von RT erhält man durch Umdrehen aller Richtungen.
R}.
Ist R eine Abbildung, so ist RT = R-1.
Die Bezeichnung rührt daher, daß die Matrix von RT
gleich der transponierten Matrix von R ist. Den gerichteten Graphen
von RT erhält man durch Umdrehen aller Richtungen.
![]() b
b ![]() A:
(a,b)
A:
(a,b) ![]() R
R ![]() (b,c)
(b,c) ![]() S}. Dummerweise ist die Konvention genau
umgekehrt wie bei Abbildungen: Sind f und g Abbildungen, so ist
f ° g (als Relationenprodukt) = g ° f (als Komposition von Abbildungen),
also aufpassen!
S}. Dummerweise ist die Konvention genau
umgekehrt wie bei Abbildungen: Sind f und g Abbildungen, so ist
f ° g (als Relationenprodukt) = g ° f (als Komposition von Abbildungen),
also aufpassen!
![]() A
mit (a,b)
A
mit (a,b) ![]() R und (b,c)
R und (b,c) ![]() R
zählen).
Man kann R ° S auch aus der Digraphendarstellung ablesen:
Färbt man alle gerichtete Kanten von R rot
und alle gerichtete Kanten von S schwarz,
dann ist ganu dann (x,y)
R
zählen).
Man kann R ° S auch aus der Digraphendarstellung ablesen:
Färbt man alle gerichtete Kanten von R rot
und alle gerichtete Kanten von S schwarz,
dann ist ganu dann (x,y) ![]() R ° S falls man durch
einen "Doppelzug", erst entlang einer roten Kante,
danach entlang einer schwarzen Kante,
von x nach y kommen kann.
R ° S falls man durch
einen "Doppelzug", erst entlang einer roten Kante,
danach entlang einer schwarzen Kante,
von x nach y kommen kann.
![]() Die transitive Hülle jeder binären Relation auf einer Menge
ist transitiv.
Die transitive Hülle jeder binären Relation auf einer Menge
ist transitiv.
 D2:
D2: D3:
D3:
 D5:
D5: D6:
D6:
