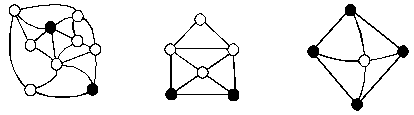

Wieso kann eine Ameise die Kanten eines Oktaeders so ablaufen, daß jede Kante genau einmal durchlaufen wird, während das mit einem Würfel nicht klappt? Und wo endet die Reise der Ameise auf dem Oktaeder?
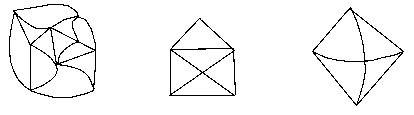
Welche der folgenden Figuren läßt sich ohne abzusetzen in einem Zug zeichnen?

|
Gegeben sei ein (ungerichteter)
Graph, gegeben durch Eckenmenge V
und Kantenmenge E.
Eine endliche Folge v1,v2,...,vt
von Ecken heißt Euler'sche Linie,
falls E = {vjvj+1 | 1 |
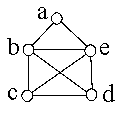 Die Frage, welche Graphen solche Linien erlauben, wurde schon
1736 von Euler vollständig
beantwortet. Ausgelöst wurde
Euler's Untersuchung durch die Frage, ob im damaligen
Königsberg ein Spaziergang möglich sei, bei dem jede Brücke
genau einmal überschritten wird, dem sogenannten
Königsberger Brückenproblem.
Die Frage, welche Graphen solche Linien erlauben, wurde schon
1736 von Euler vollständig
beantwortet. Ausgelöst wurde
Euler's Untersuchung durch die Frage, ob im damaligen
Königsberg ein Spaziergang möglich sei, bei dem jede Brücke
genau einmal überschritten wird, dem sogenannten
Königsberger Brückenproblem.
Damit läßt sich obiges Rätsel leicht auflösen: Wir erhalten Graphen aus den Zeichnungen, indem wir an allen Punkten, an denen mindestens 3 Linien zusammenstoßen, Ecken einfügen. Ecken mit geradem Grad sind weiß , Ecken ungeraden Grades schwarz gefärbt.