
DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000
Färbung von Graphen
Sieben Vorlesungen sollen jeweils
an einem Samstag die Abschlußklausur schreiben.
Vorlesung VA wird von den Studenten S1, S2, S3, S4 besucht,
Vorlesung VB wird von den Studenten S1, S5, S6, S7 besucht,
Vorlesung VC wird von den Studenten S7, S8, S9, S10 besucht,
Vorlesung VD wird von den Studenten S9, S10, S11, S12 besucht,
Vorlesung VE wird von den Studenten S5, S6, S12, S13 besucht,
Vorlesung VF wird von den Studenten S8, S13, S14, S15 besucht,
Vorlesung VG wird von den Studenten S3, S11, S15, S16 besucht.
An wievielen Samstagen mindestens muß der Pförtner
die Universität aufschließen?
Eine Teilmenge V' der Eckenmenge eines Graphen G ist
unabhängig/vollständig, falls keine zwei/je zwei
Ecken aus G benachbart sind.
G sei ein (ungerichteter)
Graph mit Eckenmenge V
und Kantenmenge E. Eine (zulässige) Färbung von G
ist eine Färbung der Ecken mit den Farben 1,2,...,k
so daß benachbarte Ecken verschiedene Farben haben.
(also ist eine (zulässige) Färbung eine Abbildung
f: V  {1,2,...,k} mit der Eigenschaft
f(x) {1,2,...,k} mit der Eigenschaft
f(x) 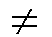 f(y) für alle
Ecken x,y mit {x,y} f(y) für alle
Ecken x,y mit {x,y}  E.) E.)
Die kleinste natürliche Zahl k für die G eine
zulässige Färbung mit Farben 1,2, ... , k hat,
wird die chromatische Zahl 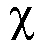 (G)
genannt. (G)
genannt.
|
Beachten Sie, daß bei jeder zulässigen Färbung
f: V  {1,2,...,k} die Urbildmengen
f-1(1), f-1(2), ... , f-1(k)
eine Partition der Eckenmenge in unabhängige Mengen
ist.
In diesem Applet können Sie
versuchen 3 Graphen, darunter der aus obigem Beispiel entstehende,
mit möglichst wenig Farben (zulässig) zu färben.
{1,2,...,k} die Urbildmengen
f-1(1), f-1(2), ... , f-1(k)
eine Partition der Eckenmenge in unabhängige Mengen
ist.
In diesem Applet können Sie
versuchen 3 Graphen, darunter der aus obigem Beispiel entstehende,
mit möglichst wenig Farben (zulässig) zu färben.
Ein Graph ist genau dann mit nur einer Farbe färbbar, falls
es überhaupt keine Kanten gibt. Ein Graph ist mit zwei
Farben färbbar, falls es eine Bipartition in zwei unabhängige
Mengen gibt, d.h. falls G
bipartit ist.
Leider lassen sich 3-färbbare Graphen schon nicht mehr
gut erkennen, das Problem ist NP-vollständig.
Den (bipartiten) Würfelgraphen rechts können Sie durch Anklicken der
Ecken färben. Es wird jeweils die hellste noch mögliche
Farbe verwendet, wobei die Farbenfolge "orange", "rot",
"blau" und "schwarz" ist. In den meisten Fällen werden
Sie zwei Farben brauchen, aber es gibt auch Anklickreihenfolgen
(welche?), bei denen der Computer 4 Farben verwenden wird.
Obwohl diese Prozedur also nicht immer das optimale Ergebnis liefert,
ist die Methode interessant:
|
Greedy-Algorithmus
Wir ordnen die Ecken irgendwie an. Dann färben wir die Ecken
nacheinander, jeweils mit der kleinstmöglichen Farbe
(die Farben seien die Zahlen 1,2,3,...).
|
Natürlich hängt die Zahl der verwendeten
Farben von der gewählten Anordnung der Ecken ab,
da aber jede Ecke x höchstens dG(x)
schon gefärbte Nachbarn hat, ist eine der Farben
{1,2,...,dG(x)+1} für x möglich.

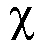 (G)
(G)  maxx dG(x) + 1.
maxx dG(x) + 1.
Das Ergebnis kann man noch minimal verbessern:
 Satz von Brooks (1941)
Jeder endliche zusammenhängende Graph, der weder vollständig
ist, noch ein Kreis ungerader Länge, lässt sich mit
maxx
Satz von Brooks (1941)
Jeder endliche zusammenhängende Graph, der weder vollständig
ist, noch ein Kreis ungerader Länge, lässt sich mit
maxx V
dG(x) Farben zulässig färben. V
dG(x) Farben zulässig färben.
|
Enthält ein Graph einen vollständigen Teilgraphen
mit k Ecken, so gibt es jedenfalls keine zulässige Färbung
von G mit weniger als k Farben, d.h.

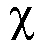 (G)
(G)
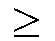
 (G),
wobei
(G),
wobei  (G) die maximale Kardinalität
eines vollständigen Teilgraphen in G ist.
(G) die maximale Kardinalität
eines vollständigen Teilgraphen in G ist.
Die beiden Parameter können verschieden sein
(ungerade Kreise), aber in den folgenden Beispielen
haben wir Gleichheit:
Übungsaufgabe:
Der Vergleichbarkeitsgraph bzw. Unvergleichbarkeitsgraph
einer geordneten Menge
(M, ) hat M als Eckenmenge.
Verschiedene Elemente x und y von M sind in G adjazent, falls
sie bzgl. "
) hat M als Eckenmenge.
Verschiedene Elemente x und y von M sind in G adjazent, falls
sie bzgl. " "
vergleichbar bzw. unvergleichbar sind.
"
vergleichbar bzw. unvergleichbar sind.
(a)
Zeigen Sie, daß sich jeder Vergleichbarkeitsgraph
G mit  (G) Farben zulässig färben
lässt.
(G) Farben zulässig färben
lässt.
(b)
Zeigen Sie, daß sich jeder Unvergleichbarkeitsgraph
G mit  (G) Farben zulässig färben
lässt.
(G) Farben zulässig färben
lässt.
Beweis: G sei ein unendlicher Graph mit Eckenmenge V.
Fund k sei eine feste natürliche Zahl.
Für x  V und
1 V und
1  i i  k
sei F(x,i) die Aussage
"x ist mit Farbe i gefärbt".
G ist genau dann k-färbbar, wenn die unendliche Menge
Xk von Aussagen k
sei F(x,i) die Aussage
"x ist mit Farbe i gefärbt".
G ist genau dann k-färbbar, wenn die unendliche Menge
Xk von Aussagen
{
F(x,1) 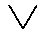 F(x,2) F(x,2) 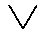 ... ...
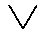 F(x,k),
/ x F(x,k),
/ x  V
} V
}

{
¬ F(x,i) 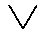 ¬ F(x,j)
/ x ¬ F(x,j)
/ x  V,
1 V,
1  i < j i < j  k
} k
}

{
¬ F(x,i) 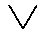 ¬ F(y,i)
/ x ¬ F(y,i)
/ x  V,
1 V,
1  i i  k
}
erfüllbar ist.
(Genauso sieht man, daß man im endlichen Fall das Problem, ob
ein Graph k-färbbar ist., auf
k-SAT zurückführen kann). k
}
erfüllbar ist.
(Genauso sieht man, daß man im endlichen Fall das Problem, ob
ein Graph k-färbbar ist., auf
k-SAT zurückführen kann).
Ist Xk
unerfüllbar (d.h. der Graph nicht mit k Farben
zulässig färbbar),
so ist nach dem
Kompaktheitssatz
(in aussagenlogischer Version)
sogar eine endliche Teilmenge davon unerfüllbar.
W sei die endliche(!) Menge aller in diesen endlich vielen
Aussagen vorkommenden Ecken. Unerfüllbarkeit dieser endlich vielen
Aussagen impliziert, daß der endliche Teilgraph von G
mit Eckenmenge W, bei denen zwei verschiedene Ecken genau dann
benachbart sind, falls sie in G benachbart waren,
auch nicht mit k Farben zulässig färbbar, wäre,
im Widerspruch zur Voraussetzung.
|
Besonders vorangetrieben wurde die Theorie der Färbungen
durch die berühmte Vierfarbenvermutung.
Sie besagt, daß jede politische Landkarte, bei der alle Länder
zusammenhängend sind, so mit 4 Farben gefärbt werden kann,
daß Länder mit gemeinsamer Grenzlinie immer verschieden
gefärbt werden können. Anders ausgedrückt, der (ebene!)
Nachbarschaftsgraph, dessen Ecken die Länder sind, und bei dem
Länder benachbart sind, falls sie eine gemeinsame Grenzlinie haben,
ist mit 4 Farben zulässig färbbar.
Hier ist eine ausführliche
externe Seite über die Geschichte des Viefarbensatzes.
Hier eine sehr farbige "Seite" zum
Vierfarbensatz, wieder
von der Universität/Gesamthochschule Wuppertal.
Erich Prisner
erstellt im Mai 2000.
