DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000

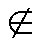• Mengen sind "ungeordnete Ansammlungen" von Elementen. Enthält Menge M das Element x schreiben wir x M, sonst x M.
• Extensionalität: Zwei Mengen sind genau dann gleich, wenn sie dieselben Elemente enthalten.
• Menge A ist eine Teilmenge von Menge B, A B, falls jedes Element von A auch in B liegt. Zwei Mengen A und B sind genau dann gleich, falls A B und B A gilt.
• Es gibt eine Menge ohne Elemente, sie wird als leere Menge bezeichnet.
• Oft geben wir Mengen durch Eigenschaften ihrer Elemente an. Genauer: Ist P(x) eine Eigenschaft, die Elemente von M haben können, so ist {x M: P(x)} die Menge aller Elemente von M, die Eigenschaft P(x) haben.
• Mengen können auch Elemente anderer Mengen sein. Z.B. gibt es für jede Menge M eine Menge P(M) aller Teilmengen von M. Diese wird die Potenzmenge von M genannt.
• Der Durchschnitt A B zweier Mengen A und B ist die Menge, die alle Elemente enthält, die sowohl in A als auch in B vorkommen. Die Vereinigung A B enthält alle Elemente, die in A oder in B vorkommen. Die Mengendifferenz A \ B enthält alle Elemente von A, die nicht in B liegen.
• Genauso werden Durchschnitt 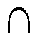_{i I} A_i und Vereinigung 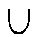_{i I} A_i von beliebig vielen Mengen gebildet.
• Das kartesische Produkt A × B zweier Mengen A und B enthält alle geordneten Paare (a,b) mit a A und b B.
• Bei unserer zu naiver Behandlung von Mengen können Widersprüche auftreten. Kann es die Menge aller Mengen, die sich nicht selbst enthalten, geben? Man kann es aber richtig machen, indem man genau definiert, welche Mengenbildungen erlaubt sind (axiomatische Mengenlehre).