
DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000
Ordinalzahlen
Die Idee
Die natürliche Zahlen kommen in zwei Geschmacksrichtungen vor:
"one, two, three, ..." bezieht sich auf Anzahlen.
"first, second, third, ..." beschreibt dagegen einen Rang.
D.h. nach jeder Zahl m kommt ein unmittelbarer Nachfolger m' = m+1.
Diese zweite Verwendung der natürlichen Zahlen lässt sich
auf die sogenannten Ordinalzahlen verallgemeinern.
Ordinalzahlen sollen Mengen sein.
Wie kann man, für eine gegebene Kardinalzahl (Menge) M
einen Nachfolger M' definieren? Man könnte natürlich
einfach ein weiteres Element in die Menge legen, nur welches
Element, wo nehmen wir es her? Es soll ja nicht schon in M liegen!
Die natürlichen Zahlen, selbst die
reellen Zahlen könnten vielleicht einmal aufgebraucht sein
(wenn wir das Nachfolger-Spiel nur genügend lang weiterspielen).
Wie wär's mit M'= M  {M}?
{M}?
Das bedeutet, daß alle Elemente der entstehenden Ordinalzahlen
wieder Mengen, sogar Ordinalzahlen, sind. 0,1,2,3,... wären
(und sind für die Dauer dieses Kapitels) Mengen, und wir
erhalten
1 = 0' = {0},
2 = 1' = {0,1},
3 = 2' = {0,1,2}, usw.
bzw. eingesetzt
1 = {0},
2 = {0,{0}
},
3 = {0,{0},
{0,1}},
4 = {0,{0},{0,1},
{0,1,2}}, ... also
1 = {0},
2 = {0,{0}},
3 = {0,{0},{0,
{0}}},
4 = {0,{0},{0,
{0}},{0,
{0},{0,
{0}}}}, ...
Es bleibt eigentlich nur noch die "0" übrig.
Sie soll auch eine Menge sein---die einfachste Menge ist
natürlich die leere Menge Ø, weshalb
wir 0 := Ø setzen.
Ordinalzahlen
Bei obiger Konstruktion ist nicht klar, wie "lange" man das
Nachfolger-Spiel betreiben kann oder muss. Die Menge
N={0,1,2,...} aller natürlicher Zahlen
ist etwa nicht unmittelbarer Nachfolger einer Ordinalzahl, trotzdem soll
es eine Ordinalzahl sein.Deshalb wollen wir
Ordinalzahlen über den Begriff der transitiven Menge definieren.
|
Eine Menge X ist transitiv wenn jedes Element
von X eine Teilmenge von X ist.
|
Mit anderen Worten ist X transitiv, wenn stets
aus Z  Y
Y  X
folgt Z
X
folgt Z  X.
Transitive Mengen haben die merkwürdige Eigenschaft, daß
alle ihre Elemente wieder Mengen sind, aber auch die Elemente
dieser Teilmengen müssen Teilmengen sein, usw.
Machen Sie sich bitte klar, daß deshalb bei der Beschreibung
transitiver Mengen nur die Symbole "{", "}", "," und
"Ø" vorkommen können.
Aber Vorsicht, nicht jede Menge, die sich so schreiben läßt,
ist schon transitiv.
X.
Transitive Mengen haben die merkwürdige Eigenschaft, daß
alle ihre Elemente wieder Mengen sind, aber auch die Elemente
dieser Teilmengen müssen Teilmengen sein, usw.
Machen Sie sich bitte klar, daß deshalb bei der Beschreibung
transitiver Mengen nur die Symbole "{", "}", "," und
"Ø" vorkommen können.
Aber Vorsicht, nicht jede Menge, die sich so schreiben läßt,
ist schon transitiv.
Beispiele von transitiven Mengen sind
{Ø,{Ø}}
oder auch
{
Ø,
{Ø},
{{Ø}},
{{{Ø}},{Ø}}
}
|
Eine Ordinalzahl ist eine transitive Menge, bei der auch
jedes Element transitiv ist.
|
Mit obiger Interpretation
1 = {Ø},
2 = {Ø,{Ø}},
3 = {Ø,{Ø},
{Ø,{Ø}}}, ...
der natürlichen Zahlen durch transitive Mengen
betrachten wir die (transitive) Menge N
aller natürlichen Zahlen.
Sie ist eine Ordinalzahl.
In der Theorie der Ordinalzahlen verwendet man meistens
den Buchstaben  statt N, um die
Ordinalzahl von der Kardinalzahl zu unterscheiden.
statt N, um die
Ordinalzahl von der Kardinalzahl zu unterscheiden.
Nun haben wir schon die Ordinalzahlen 0, 1, 2, ... ,
 . Weitere Ordinalzahlen finden wir
wieder durch die Nachfolgerkonstruktion, denn es gilt:
. Weitere Ordinalzahlen finden wir
wieder durch die Nachfolgerkonstruktion, denn es gilt:
 Ist X eine Ordinalzahl, so auch die Menge X' :=
X
Ist X eine Ordinalzahl, so auch die Menge X' :=
X  {X}. {X}.
|
Beweis: Wir betrachten eine Element A von X'. Ist A Element von
X, so ist es wegen der Transitivität von X
auch Teilmenge von X; X  X' impliziert
dann A X' impliziert
dann A  X'.
Da X Teilmenge von X' ist, ist der Fall A = X auch klar.
Deshalb ist X' transitiv. X'.
Da X Teilmenge von X' ist, ist der Fall A = X auch klar.
Deshalb ist X' transitiv.
X ist transitiv. Jedes weitere Element von X' ist,
als Element von X, ebenfalls transitiv.
|
Da dies das Analogon für den Nachfolger bei natürlichen
Zahlen ist, schreiben wir
X + 1 := X' := X  {X}. {X}.
|
Deshalb ist  + 1 =
+ 1 =

 {
{ } wieder eine Ordinalzahl.
Genauso kann man weitere Ordinalzahlen
} wieder eine Ordinalzahl.
Genauso kann man weitere Ordinalzahlen
 +2 :=
+2 :=  +1+1,
+1+1,
 +3 :=
+3 :=  +1+1+1, ...
bilden. Man prüft leicht nach, daß die Menge
aller bisher konstruierten Ordinalzahlen
2
+1+1+1, ...
bilden. Man prüft leicht nach, daß die Menge
aller bisher konstruierten Ordinalzahlen
2 := {0,1,2,...,
:= {0,1,2,...,  ,
,
 +1,
+1,  +2, ...}
wieder eine Ordinalzahl ist.
Man konstruiert weiter und findet
2
+2, ...}
wieder eine Ordinalzahl ist.
Man konstruiert weiter und findet
2 +1,
2
+1,
2 +2, ... ,
m
+2, ... ,
m +k, ... .
+k, ... .
Bisher benutzten wir zwei Konstruktionsmethoden: Manche Ordinalzahlen
sind Nachfolger von anderen Ordinalzahlen, während andere
diese Eigenschaft nicht haben.
|
Eine Limeszahl ist eine Ordinalzahl, die nicht unmittelbarer
Nachfolger einer anderen Ordinalzahl ist.
|
Z.B: sind
 , 2
, 2 ,
3
,
3 , ... alles Limeszahlen.
, ... alles Limeszahlen.
Vergleich von Ordinalzahlen
Ordinalzahlen haben offensichtlich eine lineare Struktur.
Sind sie also linear geordnet? Vorsicht, das macht keinen Sinn,
die Menge aller Ordinalzahlen gibt es nicht. Aber wir werden sehen,
daß jede Ordinalzahl eine Menge von Ordinalzahlen ist,
die sogar wohlgeordnet ist.
 Jedes Element einer Ordinalzahl ist wieder eine Ordinalzahl.
Jedes Element einer Ordinalzahl ist wieder eine Ordinalzahl.
|
Beweis: Sei M Ordinalzahl und A  M.
Da M Ordinalzahl ist, ist A transitiv.
Sei B M.
Da M Ordinalzahl ist, ist A transitiv.
Sei B  A. Da M transitiv ist, folgt
B A. Da M transitiv ist, folgt
B  M und B ist deshalb auch transitiv. M und B ist deshalb auch transitiv.
|
Wir definieren für eine Menge (von Mengen) M
eine Relation "= " durch
A =
" durch
A = B falls
A = B oder A
B falls
A = B oder A  B gilt.
B gilt.
Beweis: (1) Transitivität folgt aus Obigem,
Reflexivität aus der Definition der Relation.
Antisymmetrie ergibt sich aus der Eigenschaft
daß eine Menge sich nie selbst enthalten kann (
Dies folgt aus dem sogenannten
Fundierungsaxiom der Axiomatischen Mengenlehre,
das besagt, daß jede nichtleere
Menge M eine Element a enthält, das zu M disjunkt ist.
Für jede Menge A können wir,
wieder mit Axiomen der Mengenlehre, die
Menge {A} bilden. Mit dem Fundierungsaxiom ist
A  {A} = Ø,
also A {A} = Ø,
also A 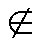 A.
). Seien also A A.
). Seien also A 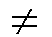 B B
 M
mit A M
mit A  B und B B und B  A.
Da M Ordinalzahl ist, muß A transitiv sein, also
A A.
Da M Ordinalzahl ist, muß A transitiv sein, also
A  A, ein Widerspruch. A, ein Widerspruch.
(2) Die Wohlordnungseigenschaft ist etwas
schwieriger
zu beweisen.
|
Ordinalzahlen sind (modulo Isomorphie) gerade die wohlgeordneten Mengen:
 Jede wohlgeordnete Menge ist zu
(genau einer) Ordinalzahl isomorph.
Jede wohlgeordnete Menge ist zu
(genau einer) Ordinalzahl isomorph.
Beweis
durch transfinite Induktion.
|
Ordinal- und Kardinalzahlen
Die Ordinalzahlen vom Typ m +k
(k,m
+k
(k,m  N) sind alle
gleichmächtig wie
N) sind alle
gleichmächtig wie
 , aber alle verschiedene
Ordinalzahlen.
Während also Ordinalzahlen und Kardinalzahlen sich im Endlichen
entsprechen, sind die Ordinalzahlen im Unendlichen
wesentlich feiner als die Kardinalzahlen.
, aber alle verschiedene
Ordinalzahlen.
Während also Ordinalzahlen und Kardinalzahlen sich im Endlichen
entsprechen, sind die Ordinalzahlen im Unendlichen
wesentlich feiner als die Kardinalzahlen.

Weiter zu
...
Erich Prisner
erstellt im Februar 2000. Zuletzt im Mai 2000 geändert.

