Logo

DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000

Normalformen

konjunktiv und disjunktiv

Für einen Typ von Aussageformen lassen sich alle erfüllenden Belegungen sofort ablesen: Ist
g(x1,x2,¼,, xn) = i Î I x1c(1,i) Ùx 2c(2,i) Ù ¼Ùxn c(n,i),
wobei alle c(k,i) Î {-1,1} sind und xi1 = xi bzw. xi-1 = Øxi gesetzt wird. Dann erfüllen genau |I| Tupel den Ausdruck, und zwar für jedes i Î I das Tupel (x1, x2, ...,xn) mit xk = w falls c(k,i)=1 und xk = f falls c(k,i)=-1. Unter anderem deshalb sind solche Ausdrücke sehr beliebt und erhalten einen schönen Namen kanonische disjunktive Normalform.
Disjunktive Normalformen sind Aussageformen der Form
g(x1,x2,¼,, xn) = i Î I x1c(1,i) Ùx 2c(2,i) Ù ¼Ùxn c(n,i),
c(k,i) Î {-1,0,1}, und xi1 = xi, xi0 = w, xi-1 = Øxi.

Analog ist eine konjunktive Normalform ein Ausdruck der Form

h(x1,x2,¼,, xn) = 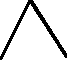i Î J x1c(1,i) Úx 2c(2,i) Ú ¼Úxn c(n,i),
wobei hier allerdings xi0 = f gesetzt wird.

In beiden Fällen ist die Form kanonisch falls alle c(k,i) ¹ 0 sind.

Für eine solche kanonische konjunktive Normalform h lassen sich alle (|J|) Belegungen die einen falschen Wert liefern direkt ablesen: Denn nach zweimaliger Anwendung der de Morganschen Regeln ist
Ø h = i Î J x1-c(1,i) Ùx 2-c(2,i) Ù ¼Ùxn -c(n,i)
eine kanonische disjunktive Normalform und wird erfüllt für alle (x1, x2, ...,xn), wenn i Î J und xk = f falls c(k,i)=1 bzw. xk = w falls c(k,i)=-1.

Umgekehrt: Haben wir eine Liste aller erfüllenden Variablentupel, dann haben wir damit auch die kanonische disjunktive Normalform. Betrachten wir beispielsweise den logischen Ausdruck f(x1,x2,x3) = x1 Å x2 Å x3. Aus der Wahrheitstafel lesen wir ab, daß es 4 erfüllende Möglichkeiten gibt:
x1=w, x2=f, x3=f,
x1=f, x2=w, x3=f,
x1=f, x2=f, x3=w,
x1=w, x2=w, x3=w.
Folglich ist x1 Å x2Åx3 = (x1ÙØx2 Ù Øx3) Ú (Øx1Ù x2 ÙØx3) Ú (Øx1Ù Øx2Ù x3) Ú (x1Ùx2 Ùx3)

Da das Prinzip allgemein funktioniert (solange die Aussageform nicht kontradiktorisch ist) erhalten wir:

Zu jeder nicht kontradiktorischen Aussageform gibt es eine gleichwertige Aussageform in kanonischer disjunktiver Normalform.
Zu jeder nicht tautologischen Aussageform gibt es eine gleichwertige Aussageform in kanonischer konjunktiver Normalform.

Beachten Sie, daß es in diesem Abschnitt zwei Arten von Beweisen gibt: Beweise, die mit Wahrheitstabellen arbeiten, und Beweise, bei denen nur die Axiome der Booleschen Algebra benutzt werden, die also für beliebige Boolesche Algebren gelten. Obwohl der Beweis eben mit Wahrheitstabellen arbeitete, werden wir sehen, daß der entsprechende Satz auch für beliebige Boolesche Algebren gilt.

Pränexe und Skolemsche Normalformen

Eine Formel einer Sprache erster Ordnung ist in pränexer Normalform, falls sie die Form Q1x1 Q2x2 ... Qnxn B hat, wobei Q1, ... Qn Quantoren sind und B quantorenfrei ist. Sie ist in Skolem'scher Normalform, falls sogar alle Quantoren der Allquantor """ sind.
Beispielsweise ist $ x " y $ z (z=x Ú R x y). in pränexer Normalform, und " x " y " z (z=x Ú R x y). sogar in Skolem'scher Normalform.

Jede Formel einer Sprache erster Ordnung ist zu einer Formel in pränexer disjunktiver Normalform (bzw. pränexer konjunktiver Normalform) äquivalent.
Beweis: Wir führen Induktion über den Formelaufbau. .......
Beispiel:

Noch angenehmer sind Formeln in Skolem'scher Normalform, Dummerweise läßt sich nicht jede Formel äquivalent in eine solche Formel umformen. ....

Zwei Formeln A und B heißen erfüllungsgleich, falls entweder beide erfüllbar sind (aber nicht notwendig im selben Modell!) oder beide unerfüllbar sind. Sie sind allgemeingültigkeitsgleich, falls ....

Zu jeder Formel einer Sprache erster Ordnung gibt es eine erfüllungsgleiche Formel (in einer Spracherweiterung) in Skolem'scher Normalform.
Weiter zur Booleschen Algebra oder zur Erfüllbarkeit
Erich Prisner
erstellt im Februar und Juni 2000.