DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000

Definition: Gegeben sei ein Verband (B,,). Falls außerdem folgende Regeln gelten (jeweils für alle a,b,c B): Distributivgesetze: a (b c) = (a b) (a c), sowie a (b c) = (a b) (a c). Existenz von 0 und 1: 0, 1 B a B: a 1 = a, a 0 = a, Existenz eines Komplements: a B ¬ a B: a ¬ a = 0, a ¬ a = 1, so nennt man (B,,) eine Boolesche Algebra

In jeder Booleschen Algebra (B,,) gilt: Doppelte Verneinung: ¬ ¬ a = a. de Morgan'sche Regeln: ¬ (a b) = ¬ a ¬ b, sowie ¬ (a b) = ¬ a ¬ b.

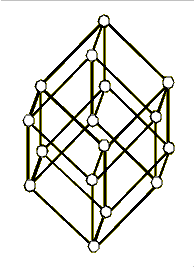
Wie sehen Boolesche Algebren aus und "wie viele" gibt es? Typische Beispiele sind Potenzmengenverbände (P(M),, ), oder als verbandsgeordnete Mengen ausgedrückt: (P(M),). Für endliches M haben diese Algebren 2ⁿ Elemente. Rechts ist das Hasse-Diagramm des entstehenden Potenzmengenverbands für ein 4-elementiges M abgebildet.
Interessanterweise is jede endliche Boolesche Algebra zu einem Potenzmengenverband isomorph. Boolesche Algebren sind also selten und sehr konkret.

Für jede endliche Boolesche Algebra (B,,) gibt es eine Menge M und eine Bijektion f: B P(M), so daß für alle x,y B gilt: f(0) = , f(1) = M, f(x y) = f(x) f(y), und f(x y) = f(x) f(y), f(¬ x) = M \ f(x). D.h. (B,,) ist zu (P(M),, ) isomorph. Beweis:

Allerdings gibt es unendliche Boolesche Algebren, die nicht zu einem Potenzmengenverband isomorph sind.

Übungsaufgabe: Betrachten Sie die Menge CF(N) aller Teilmengen S der Menge N der natürlichen Zahlen, die endlich sind oder für die das Komplement N\S endlich ist. Zeigen Sie, daß (CF(N),,) zwar eine Boolesche Algebra ist, aber zu keinem Potenzmengenverband isomorph ist.

Genauso wie kartesische Produkte von Verbänden wieder Verbände sind, sind auch kartesische Produkte von Booleschen Algebren wieder Boolesche Algebren.

Für jedes i I sei (Bi,i, i) eine Boolesche Algebra. Dann ist das kartesische Produkt i I Bi wieder eine Boolesche Algebra. Beweis:

x M

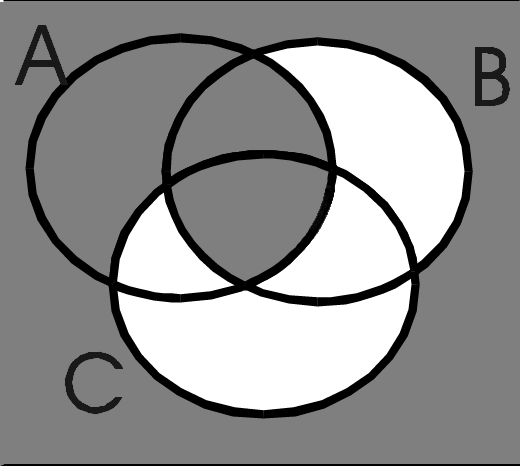A, B, C seien beliebige Teilmengen einer Menge M. Die rechts skizzierte Menge
(((A (M\B)) (M \ (C (M\A))) A ) ) (B (M\C))
läßt sich auch in der kanonischen disjunktiven Normalform
((M\A) (M\B) (M\C)) (A (M\B) (M\C)) (A B (M\C)) (A B C) ausdrücken (Vereinigung von vier der acht möglichen entstehenden Teilmengen von M). Das läßt sich verallgemeinern:

(B,,) sei eine Boolesche Algebra. f: Bn B sei eine n-stellige Verknüpfung auf B. Bildet f nicht alles auf 0 ab, so läßt sich f als kanonische disjunktive Normalform ausdrücken. Bildet f nicht alles auf 1 ab, so läßt sich f als kanonische konjunktive Normalform ausdrücken.

Beweis für endliches B: Nach obigem Satz können wir uns auf Boolesche Algebren der Form i M (P({x}),, ) beschränken. Dann können wir einfach in jeder Koordinate das Resultat für 2-elementige Boolesche Algebren (Aussagenalgebren) benutzen. Beweis für beliebiges B.

Satz von Sperner Wir betrachten den Potenzmengenverband (P({1,2,...,n}), ,). Dann ist die maximale Anzahl der Elemente in einer Antikette gleich ( n n/2 ) für gerades n, bzw. ( n (n+1)/2 ) für ungerades n Beweis

Test

Ist ({1,2,3,4,6,12},kgV,ggT) eine Boolesche Algebra? Ist ({1,2,3,5,6,10,15,30},kgV,ggT) eine Boolesche Algebra?