
| Definition: Eine reflexive, symmetrische und transitive binäre Relation auf einer Menge M wird Äquivalenzrelation genannt. Dann definieren wir für jedes x Î M die Menge Rx = {y Î M|(x,y) Î R}. Diese Teilmengen Rx, x Î M, von M werden Äquivalenzklassen der Äquivalenzrelation genannt. |
Eine Partition einer Menge M ist eine Menge {Pi | i Î I} paarweise disjunkter nichtleerer Teilmengen von M, deren Vereinigung gerade M ergibt.
Partitionen einer Menge "sind" Äquivalenzrelationen.
Eine k-Partition ist eine Partition der Mächtigkeit k. Wieviele k-Partitionen einer n-elementigen Menge gibt es? Diese Zahlen werden Stirling-Zahlen zweiter Art S(n,k) genannt.
Beispiele von Äquivalenzrelationen sind "äquivalent modulo k" bei natürlichen Zahlen, oder auch Äquivalenz von aussagelogischen Formeln. In beiden Beispielen haben wir auch noch Verknüpfungen, "+" und "*" im ersten Beispiel, im zweiten Beispiel werden Formeln durch Junktoren zu grösseren Formeln verknüpft. Die Verknüpfungen sind nun verträglich mit der entsprechenden Äquivalenzrelation: Sind a und b kongruent modulo k, und c und d kongruent modulo k, so sind auch a+c und b+d kongruent modulo k, ebenso wie a*c und b*d. Bei den Formeln sind (nach der zweiten Substitutionsregel etwa A Ú C und B Ú D äquivalent, falls A und B äquivalent sind und C und D äquivalent sind (und ebenso mit anderen Junktoren). Es gibt für solche Sachverhalte natürlich wieder einen Namen:
| Sei M eine Menge mit einer binären Verknüpfung "$". Eine Äquivalenzrelation R auf M heißt Kongruenzrelation (bzgl. "$") falls sie mit "§" in dem Sinne verträglich ist, daß aus (a,b) Î R und (c,d) Î R immer auch (a§c,b§d) Î R folgt. |
| Deren Äquivalenzklassen werden die starken (Zusammenhangs-) Komponenten von R genannt. |
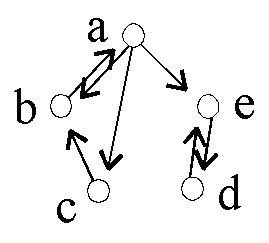 Im Beispiel rechts gibt es zwei starke Komponenten:
{a,b,c} und {d,e}.
Im Beispiel rechts gibt es zwei starke Komponenten:
{a,b,c} und {d,e}.
Übungsaufgabe:
R sei eine Relation auf einer Menge M.
M¢ sei die Menge der starken Komponenten.
Wir definieren eine Relation R¢
Í M¢×M
¢
durch (A,B) Î R¢
Û $a
Î A $b
Î B: (a,b) Î R,
die Kondensation von R.
Zeigen Sie, daß die starken Komponenten bzgl. R'
alle einelementig sind. Zeigen Sie auch
daß die Kondensation der transitiven Hülle
(R*)¢ gleich
der transitiven Hülle der Kondensation (R¢)
* ist.
 Die Menge aller Partitionen einer festen Menge M
läßt sich ordnen:
Wir nennen eine Partition {A1, A2, ... , Ak}
gröber als die Partition
{B1, B2, ... , Bm},
falls es eine Abbildung
f: {1,2,...,m} ® {1,2,...k} gibt,
so daß für jedes
i Bi Í Af(i) gilt.
Insbesondere ist dann f surjektiv und deshalb
k £ m.
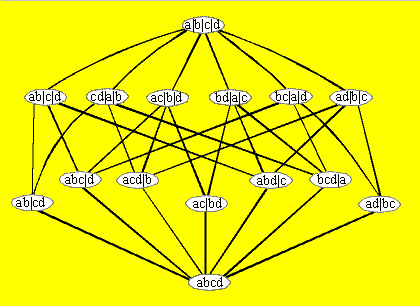
Diese Relation ist eine Ordnungsrelation. Rechts ist das Hasse-Diagramm
für die Menge M={a,b,c,d} abgebildet, wobei die Schreibweise
ad|b|c eine Abkürzung für die Partition
{{a,d},{b},{c}} ist.
Die Menge aller Partitionen einer festen Menge M
läßt sich ordnen:
Wir nennen eine Partition {A1, A2, ... , Ak}
gröber als die Partition
{B1, B2, ... , Bm},
falls es eine Abbildung
f: {1,2,...,m} ® {1,2,...k} gibt,
so daß für jedes
i Bi Í Af(i) gilt.
Insbesondere ist dann f surjektiv und deshalb
k £ m.
Diese Relation ist eine Ordnungsrelation. Rechts ist das Hasse-Diagramm
für die Menge M={a,b,c,d} abgebildet, wobei die Schreibweise
ad|b|c eine Abkürzung für die Partition
{{a,d},{b},{c}} ist.