
DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000
Binäre Relationen
auf einer Menge
Inhalt:
Binäre Relationen R Í A ×A
auf einer Menge A
werden manchmal auch homogene
(binäre) Relationen genannt. Die (Nicht-) Gültigkeit einiger
Eigenschaften entscheidet, ob die Relation
Ordnungsrelation,
Äquivalenzrelation, oder ein
(ungerichteter) Graph ist.
Wir werden zwei Möglichkeiten solche Relationen darzustellen
kennenlernen---einerseits durch quadratische 0-1 Matrizen, andererseits
als gerichtete Graphen.
Relationen auf einer festen Menge A kann man schneiden und vereinigen, und man
kann auch das Komplement bilden. Ausserdem kann man Transponieren,
und Komponieren; tatsächlich hat die Menge aller Relationen
auf A einige interessante Eigenschaften bzgl. dieser Operationen.
Definition:
Eine binäre Relation R Í A ×A
auf A heißt
- reflexiv falls (a,a) Î R
für jedes a Î A gilt.
- irreflexiv falls für kein a Î A
gilt (a,a) Î R.
- symmetrisch falls aus (a,b) Î R
immer auch (b,a) Î R folgt.
- antisymmetrisch falls aus
(a,b), (b,a) Î R folgt a= b.
- transitiv falls aus (a,b) Î R und
(b,c) Î R immer auch
(a,c) Î R folgt.
|
Die natürlichste binäre Relation auf einer Menge A
ist die Identität
(oder Gleichheitsrelation, Diagonale)
idA = {(a,a) | a Î A}.
Darstellung binärer Relationen
Binäre Relationen auf endlichen Mengen M
können auf zwei Arten visualiert werden.
Erstens durch quadratische |M| × |M| 0-1 Matrizen.
Zuerst muß man die Elemente von M als
x1,x2,...,x|M|
durchnummerieren. Für i,j Î {1,2,..|M|}
definiert man ai,j = 1
falls (xi,xj) Î R,
und andernfalls ai,j = 0.
Die zweite
Visualisierungsmöglichkeit benutzt sogenannte
gerichtete Graphen oder (Digraphen).
Die Elemente von M werden aufs Blatt
gezeichnet und Ecken genannt.
Nun zieht man einen Pfeil (gerichtete Kante)
von x nach y wenn
(x,y) Î R ist. Eventuelle
gerichtete Kanten von x nach x werden wegen ihrer Bumerangnatur
Schlingen genannt.
Natürlich kann dieselbe Relation, d.h. derselbe Digraph
sehr verschieden gezeichnet werden.
|
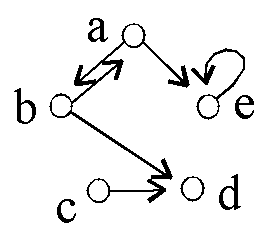
Beispiel:
Sei M = {a,b,c,d,e} und R={(a,b),(a,e),(b,a),(b,d),(c,d),(e,e)}.
Hier ist die Matrix (für Reihenfolge a,b,c,d,e)
und der gerichtete Graph.
|
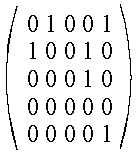 |
 |
Homomorphismen/Isomorphie
Wie bei jeder mathematischen Struktur gibt es auch
hier den Begriff des Homomorphismus und der Isomorphie.
Ein Homomorphismus
von einer Relation
R Í A ×A
auf eine Relation
R' Í A' ×A'
ist eine Abbildung f: A ® A'
mit der Eigenschaft daß aus
(x,y) Î R
stets (f(x),f(y)) Î R' folgt.
Zwei Relationen R Í A ×A
und R' Í A' ×A' sind
isomorph
wenn es eine bijektive Abbildung f: A ® A'
gibt, so daß sowohl f als auch f-1
Homomorphismen sind.
Isomorphe binäre Relationen sind bis auf
Benennung der Elemente dieselben Strukturen.
Aus gegebenen Relationen lassen sich neue bilden.
Einerseits durch Durchschnitts-, Vereinigungs- und Komplementsbildung
(wir setzen ØR := (A ×A) \ R),
denn Relationen sind ja Mengen,
andererseits auch durch folgende Operationen:
Die Transposition oder inverse Relation RT
zu einer Relation R auf A ist definiert als
RT = {(b,a) | (a,b) Î R}.
Ist R eine Abbildung, so ist RT = R-1.
Die Bezeichnung rührt daher, daß die Matrix von RT
gleich der transponierten Matrix von R ist. Den gerichteten Graphen
von RT erhält man durch Umdrehen aller Richtungen.
Sind R und S Relationen auf einer Menge A,
so ist die Komposition (das Relationenprodukt)
R ° S = {(a,c) | $ b Î A:
(a,b) Î R Ù
(b,c) Î S}. Dummerweise ist die Konvention genau
umgekehrt wie bei Abbildungen: Sind f und g Abbildungen, so ist
f ° g (als Relationenprodukt) = g ° f (als Komposition von Abbildungen),
also aufpassen!
Die Matrix von R ° S ist das Matrizenprodukt der Matrizen von R und S,
wenn man beim Addieren "1 + 1 = 1" beachtet
(man möchte ja wieder eine 0-1 Matrix erhalten---andernfalls
würde man die Zahl der b Î A
mit (a,b) Î R und (b,c) Î R
zählen).
Man kann R ° S auch aus der Digraphendarstellung ablesen:
Färbt man alle gerichtete Kanten von R rot
und alle gerichtete Kanten von S schwarz,
dann ist ganu dann (x,y) Î R ° S falls man durch
einen "Doppelzug", erst entlang einer roten Kante,
danach entlang einer schwarzen Kante,
von x nach y kommen kann.
R ist genau dann
- reflexiv, wenn idA Í R,
- irreflexiv, falls idA Ç R =
Æ,
- symmetrisch, falls R = RT,
- antisymmetrisch, wenn R Ç RT
Í idA,
- transitiv, falls R ° R Í R.
Relationenalgebra
Wir betrachten die Menge aller Relationen auf einer festen Menge A.
Mit den drei ausgezeichneten Relationen
Æ, idA, sowie
1A := A ×A erhalten wir:
- (RT)T = R,
- (ØR)T = Ø(RT),
- idAT = idA,
ÆT = Æ,
1AT = 1A,
- (Q ° R) ° S = Q ° (R ° S) (Assoziativgesetz),
- idA ° R = R ° idA = R,
- 1A ° R ° 1A = 1A
für jedes R ¹
Æ ("Tarski-Regel"),
- (R ° S)T = ST ° RT (vgl. Lin.Algebra),
- Q ° R Í S genau dann wenn
QT ° ØS Í
Ø R genau dann wenn
ØS ° RT
Í Ø Q ("Schröder-Umformung")
Beweis,
Beispiel
- (Q ° R) Ç S Í
(Q Ç (S ° RT)) °
(R Ç (QT ° S)) ("Dedekind-Formel"),
Beweis
- R ° Æ = Æ ° R = Æ,
- Wenn P Í Q und R Í S,
dann P ° R Í Q ° S,
- Q ° (R Ç S) =
(Q ° R) Ç (Q ° S) und
Q ° (R È S) = (Q ° R) È (Q ° S)
(Distributivgesetze mit °).
Hüllen
Für jede Relation R Í A ×A
ist R È idA reflexiv und
R È RT symmetrisch. Die
Relationen sind die kleinsten reflexiven bzw. symmetrischen Relationen auf A,
die R enthalten. Ähnliches ist auch für "transitiv" möglich:
|
Die transitive Hülle R*
einer binären Relation R auf einer Menge M
wird definiert durch:
(x,y) Î R*
Û $k
Î N0: $
z1, z2, ¼zk
Î M: (x,z1),
(z1,z2),
¼, (zk-
1,zk),
(zk,y) Î R.
|
Definiert man R0 = idM
und Rn+1 = Rn ° R,
dann kann man die transitive Hülle auch so ausdrücken:
R* = È
n ³ 0 Rn.
Der Name ist gerechtfertigt, denn sind (x,y), (y,w)
Î R*, d.h.
gibt es natürliche Zahlen k, t ³ 0
und
z1, z2, ¼zk,
u1, u2, ¼ut
Î M: mit (x,z1),
(z1,z2),
¼, (zk-
1,zk),
(zk,y) Î R,
und (y,u1),
(u1,u2),
¼, (ut-
1,ut) Î R,
(ut,w), so ist ja offenbar damit auch
(x,w) Î R*
 Die transitive Hülle jeder binären Relation auf einer Menge
ist transitiv.
Die transitive Hülle jeder binären Relation auf einer Menge
ist transitiv.
Test
Gegeben sind 6 binäre Relationen auf {a,b,c,d,e}:
D1: D2:
D2: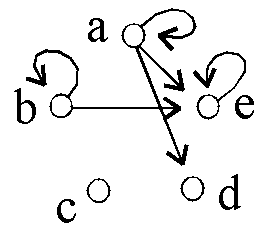 D3:
D3: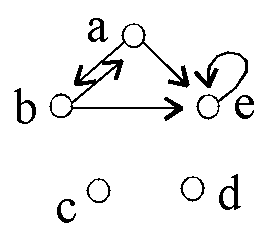
D4: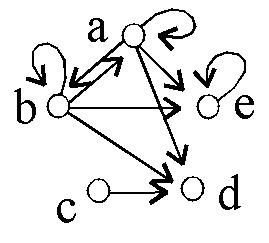 D5:
D5: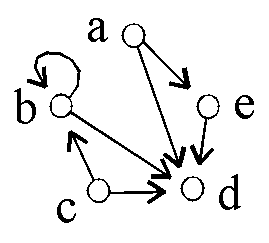 D6:
D6: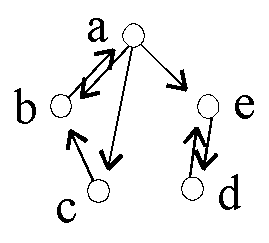
|
D1* = ? |
|
|
Was ist D1 ° D1? |
|
|
irreflexiv ist ... |
|
|
transitiv ist ... |
|
|

|
Die wichtigsten biären Relationen auf einer Menge sind
Ordnungsrelationen,
Äquivalenzrelationen und
(ungerichtete) Graphen.
Erich Prisner
erstellt im Februar 2000, zuletzt geändert am 11. April 2000.
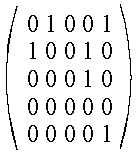


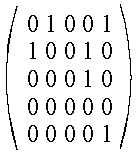

![]() Die transitive Hülle jeder binären Relation auf einer Menge
ist transitiv.
Die transitive Hülle jeder binären Relation auf einer Menge
ist transitiv.
 D2:
D2: D3:
D3:
 D5:
D5: D6:
D6:
