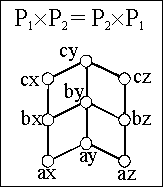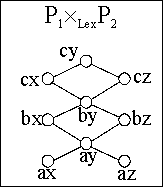Logo

DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000

Anmerkungen

Beispiele: "Paris ist die Hauptstadt Frankreichs". Keine Aussagen in diesem Sinn sind z.B. selbstbezügliche Sätze wie: "Dieser Satz ist falsch". Oder "Dieser Satz enthält elf Worte". Liessen wir den letzten Satz als Aussage zu, bekämen wir Probleme bei "Paris ist die Hauptstadt Frankreichs und dieser Satz enthält elf Worte"
Induktive Definition der Syntax von Formeln:
Trotzdem sind auch im Unendlichen Teilmengenverbände wichtig. Nach dem Stoneschen Darstellungssatz gibt es zu jeder Booleschen Algebra (B,Ù,Ú) eine Menge M sowie eine bzgl. "È", "Ç" und Komplement abgeschlossenen Menge F Í P(M) von Teilmengen von M, so daß (B,Ù,Ú) zu (F,Ç, È) isomorph ist.
Beispielsweise kann man so beweisen, daß sich jede natürliche Zahl ³14 als 3a + 8b mit a,b ³ 1, schreiben läßt. Angenommen nicht, dann ...
Da wir davon ausgehen können, daß jede 6-elementige Teilmenge von {1,2,...,49} gleiche Chancen hat, gezogen zu werden (warum eigentlich?), müssen wir nur den Quotienten aus der Anzahl a der 6-elementigen Teilmengen, bei denen der Abstand zweier Elemente immer größer als 1 ist und (49 über 6) bilden. ........... Also ist die Wahrscheinlichkeit für das oben beschriebene Ereignis (44 über 6)/(49 über 6) = (44*43*42*41*40*39)/(49*48*47*46*45*44) » 0.5048
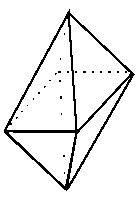Oktaeder Der Oktaeder
Zwei geordnete Mengen:
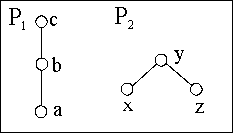
und die verschiedenen möglichen Produkte
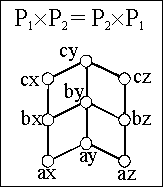
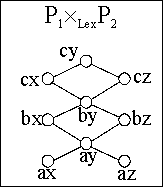
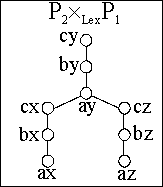
Gäbe es zwei größte Elemente x,y Î A von A, dann wäre insbesondere auch x ³ y und y ³ x. Wegen der Antisymmetrie folgt daraus x = y.
Eine Möglichkeit ist: Wir starten mit der (nichtleeren) Menge {a1,1, ... , at(1),1} aller minimalen Elemente der geordneten Menge (M,£) und schreiben jedes ai,1 an die Stelle (i,1) der Ebene. Im zweiten Schritt betrachten wir die Menge {a1,2, ... , at(2),2} aller minimalen Elemente der durch "£" geordneten Teilmenge M \ {a1,1, ... , at(1),1} und schreiben jedes ai,2 an die Stelle (i,2) der Ebene. Im kten Schritt betrachten wir die Menge {a1,k, ... , at(k),k} aller minimalen Elemente der durch "£" geordneten Teilmenge M \ {a1,1, ... , at(k-1),k} und schreiben jedes ai,k an die Stelle (i,k) der Ebene.
Betrachten Sie die durch h(S) = A \ g(B\f(S)) definierte Abbildung h: P(A) ® P(A)
A Ú B steht für Ø(A Ù B).
A ® B steht für ( Ø A ) Ú B
$ x steht für Ø (" x).
Wir illustrieren dies durch (zugegeben etwas spezielle) Relationen: (x,y) Î B bedeute "x ist Bruder von y". (x,y) Î P bedeute "x ist Pate von y". (x,y) Î E bedeute "x ist Elternteil von y". Dann lesen sich die drei Formeln wie folgt: (vgl. Schmidt, Ströhlein, "Relationen und Graphen").
Wir verwenden etwa die sogenannte "Davis-Putnam Prozedur": Die Variablen seien (etwa als P1, P2, ... Pn) linear geordnet.
  1. For (i=1; i < n+1; i++)
    1. Füge alle Resolventen über Pi (d.h. alle Klauseln, die man aus Klauseln C È {Pi} und D È {ØPi} erhält) hinzu.
    2. Streiche alle Tautologien und alle Klauseln, die Pi oder ØPi enthalten.
  2. Haben wir keine Klauseln mehr, ist die ursprüngliche Klauselmenge erfüllbar. Andernfalls ist noch die leere Klausel übrig, und die ursprüngliche Klauselmenge ist nicht erfüllbar.
Tseitin's Theorem: Wir starten mit einem Graphen G=(V,E), dessen Ecken mit Nullen und Einsen "gelabelt" sind. Alle Kanten werden mit verschiedenen Aussagenvariablen bezeichnet. P1, P2, ... Pt seinen alle Kanten die an einer festen Ecke liegen. und diese Ecke habe Label 1. Dann Fügen wir alle Klauseln, die aus {P1,P2,...,Pt} durch Negation ungerade vieler Variablen entstehen, zu unserer Klauselmenge hinzu. Hat die Ecke aber Label 0, so fügen wir alle Klauseln, die aus {P1,P2,...,Pt} durch Negation gerade vieler Variablen entstehen, hinzu.
Die entstehene Klauselmenge (mit åxÎV 2dG(x) Klauseln) ist nach Tseitin's Theorem genau dann erfüllbar, wenn die Anzahl der mit "1" bezeichneten Ecken gerade ist.
Erich Prisner
File partially translated from TEX by T TH, version 2.53.
erstellt im Februar 2000.