DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000

Satz von Dilworth In jeder endlichen (!) geordneten Menge (M,£) ist die minimale Mächtigkeit einer Partition von M in Ketten gleich der maximalen Mächtigkeit einer Antikette.

Direkter Beweis Beweis mit dem Satz von König

Es gibt eine interessante Folgerung: Nehmen Sie entweder diese Folge von 37 Zufallszahlen, oder verändern Sie sie. Drücken Sie "Auf" bzw "Ab", so sucht der Computer alle schwach aufsteigenden bzw absteigenden Teilfolgen der Länge 6. Dabei ist a₀, a₁, a₂, a₃, a₄, a₅, a₆ schwach aufsteigend, falls a₀ £ a₁ £ a₂ £ a₃ £ a₄ £ a₅ £ a₆ gilt.

Satz von Erdös/Szekeres 1935 In jeder endlichen Folge von n2+1 natürlicher Zahlen gibt es eine schwach aufsteigende Teilfolge der Länge n+1 oder eine schwach absteigende Teilfolge der Länge n+1.

Beweis: Die Folge sei (ai)0£i £m mit m = n2. Wir ordnen die Menge {0,1, ... , n2} durch i R j falls (i £ j) und (ai £ aj). Antiketten in R entsprechen den schwach absteigenden Teilfolge, und Ketten in R entsprechen den schwach aufsteigenden Teilfolge. (Denn sei etwa {i,j,k} eine Antikette, mit etwa i < j < k. Dann ist ai > aj und aj > ak. Ist {i,j,k} Kette, so ist ai £ aj und aj £ ak) Wenn wir also keine schwach absteigende Teilfolge mit n+1 Elementen haben, dann ist die maximale Mächtigkeit einer Antikette in ({0,1,...,n2},R) höchstens n. Nach obigem Satz von Dilworth gibt es eine Überdeckung aller Elemente von R durch höchstens n Ketten---wären alle Kettenlängen kleiner als n+1, so wäre das (nach dem Taubenschlagprinzip) unmöglich.

Übungsaufgabe: In jeder endlichen geordneten Menge (M,£) ist die minimale Mächtigkeit einer Partition von M in Antiketten gleich der maximalen Mächtigkeit einer Kette. (Trotz Ähnlichkeit ist dies viel leichter zu beweisen als der Satz von Dilworth)

Reduktion auf Matchings in bipartiten Graphen

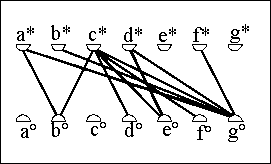
Zum Schluß zeigen wir, wie sich das Problem, Partitionen in die kleinstmögliche Zahl von Ketten zu finden, auf ein Matchingproblem in einem bipartiten Graphen zurückführen läßt. Zu einer endlichen geordneten Menge (X,£) definieren wir einen bipartiten Graphen mit zwei disjunkt gemachten Kopien von X als Eckenmenge: A = {x^°/x Î X}, B = {x^*/x Î X}. x^° und y^* sind genau dann benachbart, falls x £ y aber x ¹ y ist. 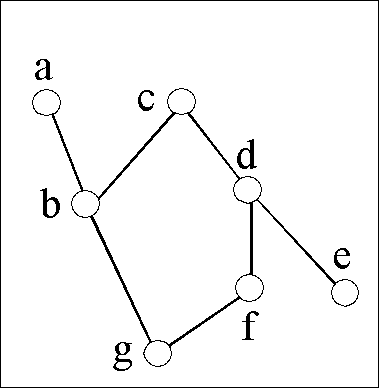Anschaulich setzen wir alle "transitiven Linien" ins Hasse-Diagramm ein, und schneiden jeden Punkt x in zwei Teile. Die oberen Hälften x^°, zusammen mit den anstossenden Linien, kommen an den unteren Bildrand, die unteren Hälften x^* an den oberen Bildrand, siehe das Beispiel.
Da bei einer Partition in Ketten jeder Punkt höchstens einmal eine Kettenverbindung nach oben und höchstens einmal eine Kettenverbindung nach unten hat, wird aus so einer Kettenpartition ein Matching im bipartiten Graphen (beachten sie, daß diese Kettenverbindungen, wie in Beispiel 2, nicht immer Hasse-Linien sind). Umgekehrt setzen sich Matchings im bipartiten Graphen zu Ketten in der geordneten Menge zusammen. Nicht jedes Element liegt dann in einer Kette, aber wir fügen einfach einelementige Ketten hinzu, bis das erreicht ist.
Bei einer Kettenpartition der n Elemente von X mit k Ketten, haben wir dann n-k Kettenlinien, also n-k Kanten im Matching im bipartiten Graphen, und umgekehrt. D.h. die kleinste Zahl von Ketten, die (X,£) partitioniert, plus der Mächtigkeit eines größten Matchings des zugeordneten bipartiten Graphen ist gleich |X|.