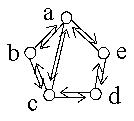
Die Zahl der Ecken ungeraden Grades in jedem endlichen Graphen ist gerade.
|
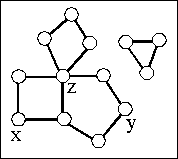
G sei ein Graph mit Eckenmenge V und Adjazenzrelation Adj.
G ist zusammenhängend, falls er, betrachtet als Digraph,
stark zusammenhängend ist.
Andernfalls werden die starken Zusammenhangskomponenten des Digraphen
als (Zusammenhangs-) Komponenten des Graphen bezeichnet.
|
|
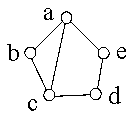
Ein Graph ist bipartit, falls es eine
Partition der Eckenmenge in zwei Mengen
A und B gibt, so daß jede Kante zwischen einer Ecke aus A
und einer Ecke aus B verläuft.
|
Bipartite Graphen lassen sich algorithmisch schnell erkennen und
die Bipartition erzeugen.
Ein Beispiel eines Problems,
das auf den zweiten Blick auf genau diese Bestimmung der
Bipartition eines bipartiten Graphen hinausläft.
Ein Weg (von x0 nach xk)
in einem Graphen ist eine endliche Folge
x0, x1, ... , xk
verschiedener Ecken bei denen je zwei aufeinanderfolgende
--- xi und xi+1 --- benachbart sind.
Bei einem Kreis müssen zusätzlich auch noch
xk und x0 benachbart sein (der Weg schließt sich
zum Kreis). Die Länge eines Kreises bzw. Weges ist gleich der Anzahl
der beteiligten Ecken, bzw. diese Anzahl minus eins.
Der Abstand dG(x,y) zweier Ecken
x und y in einem Graphen
G ist die kürzeste Länge eines Weges von x nach y falls es solche
Wege überhaupt gibt (d.h. falls x und y in derselben Komponente liegen).
Andernfalls sagen wir, der Abstand ist unendlich.
Beachten Sie folgende Eigenschaften des Abstands:
 dG(x,y)=0 genau dann wenn x = y,
dG(x,y)=0 genau dann wenn x = y,
 dG(x,y) = dG(y,x) (Symmetrie des Abstands), und
dG(x,y) = dG(y,x) (Symmetrie des Abstands), und
 dG(x,z)
£
dG(x,y) + dG(y,z)
(die sogenannte Dreiecksungleichung).
dG(x,z)
£
dG(x,y) + dG(y,z)
(die sogenannte Dreiecksungleichung).
Sehr viele Probleme, bei denen man es zuerst nicht vermutet,
lassen sich als Abstandsprobleme in Graphen umformulieren.
Beispiele sind das bekannte "Türme von Hanoi"-Rätsel,
aber etwa auch gewisse
Reihenfolgerätsel, siehe
auch diese interessante
externe Seite
über das 3-Gläser-Problem,
(das aber mit Digraphen modelliert wird).
Es gibt eine interessante Charakterisierung bipartiter Graphen mittels
Weglängen:
Beweis:
(1) Sei G bipartit mit Bipartition A und B der Eckenmenge.
Die Ecken jedes Kreises müssen abwechselnd in A und B liegen,
weshalb die Länge gerade sein muß.
(2) Ist umgekehrt G ohne Kreise ungerader Länge, dann
zeigen wir, wie wir in jeder Zusammenhangskomponente Q von G eine solche
Bipartion der Eckenmenge finden können.
Da keine Kanten zwischen Zusammenhangskomponenten verlaufen können,
setzen sich diese Bipartitionen der Komponenten zu einer zulässigen
Bipartition der gesamten Eckenmenge zusammen.
Wir wählen eine beliebige Ecke x in Q
und definieren A als die Menge der Ecken y in Q mit dG(x,y) gerade,
und B als die Menge der Ecken y in Q mit dG(x,y) ungerade.
Nehmen wir an (*), diese Bipartition der Eckenmenge von Q erfülle
obige Eigenschaft nicht, d.h. es gäbe oBdA benachbarte Ecken
y, z in A. Dann sind beide Zahlen dG(x,y) und dG(x,z)
gerade. Andererseits folgt wegen dG(y,z)=1
(mit Hilfe obiger Dreiecksungleichung)
der Widerspruch |dG(x,y) - dG(x,z)| £ 1.
Also ist Annahme (*) falsch, und die Bipartion OK.
|