Definition:
Sei M eine Menge.
Eine Abbildung C: P(M)
 P(M)
heißt Hüllenoperator,
falls für alle X, Y  M gilt:
|
Beispiel 1:
Sei V ein Vektorraum. Für A V
ist C(A) = < A > die Menge aller Linearkombinationen mit Elementen
aus A. C ist ein Hüllenoperator.
Beispiel 2: Die transitive Hülle R* einer Relation definiert einen Hüllenoperator.
Beispiel 3:
Für jede Abbildung f: A B setzen wir
C(A1) = f(f-1
(f(A1))) für A1 A
und C'(B1) =
f-1(f(f
-1(B1)))
für B1 B
Dann ist C ein Hüllenoperator auf
P(A)
und C' Hüllenoperator auf
P(B).
Beispiel 4:
Sei (M, 
) eine geordnete Menge.
Für X M ist
LOI(X) = {y 
M | 
x
X:
y x}
das von X erzeugte Ideal
Dann ist LOI ein Hüllenoperator auf
P(M).
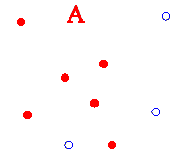Beispiel 5:
Für Teilmengen X Rn
sei
Conv(X) : =
{rx1+ ... +
rkxk | k
N, x1,
... ,xk
X,
0 r1,
... ,
rk R,
r1+ ... +rk = 1 }
die konvexe Hülle von X.
Conv ist auch ein Hüllenoperator.
Ist C ein Hüllenoperator auf einer Menge M,
so ist die Menge {C(X)|X M}
aller Hüllen bzgl.
verbandsgeordnet.
Dabei ist C(X)  C(Y) =
C(X  Y) und
C(X)  C(Y) =
C(X)  C(Y).
Beweis: |
Eine Teilmenge L
P(M)
der Potenzmenge einer Menge ist ein
abgeschlossenes System,
falls M L
ist und jeder Durchschnitt
 i
I Ai
von Elementen aus L
wieder in L liegt.
|
Für jedes abgeschlossene System
L
P(M)
können wir eine Abbildung
C: P(M)
P(M)
durch C(S) = S
A
L A definieren.
Diese Abbildung ist dann ein Hüllenoperator.
Umgekehrt ist für jeden Hüllenoperator
C: P(M)
P(M) die Bildmenge
ein abgeschlossenes System.
Abgeschlossene Systeme "sind" gerade Hüllenoperatoren: