
DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000
Praedikatenkalkuel erster Ordnung
Mathematik ist eine Sprache. Betrachtet man mathematische
Texte, so bestehen sie aus einer Mischung aus mathematischen Symbolen,
logischen Schlußweisen, und ganz viel Deutsch (oder Englisch oder ...)
Lässt sich das vielleicht noch formalisieren, so daß
alles Deutsch verschwindet und die Sprache wirklich international
verständlich ist?
Von dieser Sprache sollte man auch verlangen,
daß sie, ähnlich wie Programmiersprachen, eine feste
und überprüfbare Syntax hat.
Bei diesem Programm hilft Aussagenlogik nur ansatzweise.
Was vielleicht am meisten fehlt sind Symbole für "für alle"
und "es gibt ein".
Unser Ziel ist es, eine Sprache zu entwickeln, mit der wir Aussagen
über
mathematische Strukturen
M =
(M,R1,R2, ... , Rp,
F1,F2, ... , Fm,
c1, ... ck) formulieren können.
Dabei ist A eine Menge, die Ri sind irgendwie-stellige
Relationen auf M,
die Fi irgendwie-stellige Operationen (Verknüpfungen) auf M,
die ci sind Konstanten aus M.
Die Sprache(n)
Zuerst basteln wir eine Sprache
L,
mit der wir über obige
mathematische Struktur
M
(und ähnliche) reden können:
Die Menge 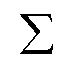 = {
= { 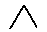 ,
,
 , (, ),
, (, ),  , = }.
der technische Zeichen umfasst:
, = }.
der technische Zeichen umfasst:
- Die Junktoren "
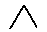 " und "
" und " "
"
- Klammern
- den Generalisator "
 "
"
- das Gleichheitszeichen "="
Wenn wir es etwas bequemer haben wollen, wählen wir etwa
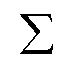 = {
= { 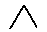 ,
,
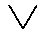 ,
,  ,
,
 , (, ),
, (, ),  ,
,
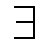 , = }.
Beachten Sie aber, daß die neu dazugenommenen Zeichen
nur Abkürzungen sind.
Diese Menge ist unabhängig davon, in welcher mathematischen Struktur
(geordnete Mengen, Graphen, Boolesche Algebren, Gruppen, ...) wir arbeiten wollen.
, = }.
Beachten Sie aber, daß die neu dazugenommenen Zeichen
nur Abkürzungen sind.
Diese Menge ist unabhängig davon, in welcher mathematischen Struktur
(geordnete Mengen, Graphen, Boolesche Algebren, Gruppen, ...) wir arbeiten wollen.
Als Zweites brauchen wir eine
Symbolmenge
S = {a, b, c, ... , R1,R2, ... , Rp,
F1,F2, ... , Fm,
c1, ... ck}.
- a,b,c, ... sind die Individuenvariablen (wobei wir davon
ausgehen, daß wir einen abzählbar unendlichen Vorrat haben,
etwa indem wir a1 ,a2, ... auch zulassen.
Diese Variablen stehen für Elemente der Menge M.
- Jedes Ri steht für eine ri-stellige Relation
auf M, d.h. für eine Teilmenge von M × M × ... × M.
- Jedes Fi steht für eine fi-stellige
Verknüpfung auf M, d.h. für eine Abbildung
M × M × ... × M
 M.
M.
- Jedes ci steht für eine Konstante aus M.
Interessant ist vielleicht, wofür wir keine Symbole haben:
Etwa für Teilmengen der Grundmenge M. Gibt es noch etwas, wofür Sie gerne
Symbole hätten?
Unsere Sprache besteht nun aus gewissen Elementen der
Menge 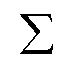 S*
aller endlichen Worte aus dem Alphabet
S*
aller endlichen Worte aus dem Alphabet
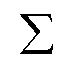 S =
S =
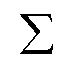
 S.
Wir unterscheiden
Terme,
Formeln und
Aussagen,
S.
Wir unterscheiden
Terme,
Formeln und
Aussagen,
Terme
Wir definieren die Menge der
Terme rekursiv:
- alle Individuenvariable aus M und alle Konstantensymbole ci
sind Terme,
- Sind t1, ... tf Terme und ist Fj
ein Symbol, das für eine f-stellige Verknüpfung steht,
so ist Fj t1 ... tf auch ein Term.
|
Formeln
Auch die Menge der
Formeln (prädikatenlogische Ausdrücke,
Aussageformen) definieren wir rekursiv:
- Sind t und s Terme, so ist "t = s" eine Formel, genauer gesagt eine Gleichung.
- Sind t1, ... , tt Terme, und steht das Symbol Rj
für eine r-stellige Relation auf M, so ist
"Rj t1 ... tr"
auch eine Formeln. Solche Formeln sowie Gleichungen werden auch
atomare Formeln (bzw. Primformeln) genannt.
- Sind A und B Formeln, dann sind "
 A" sowie
"(A A" sowie
"(A 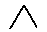 B)" Formeln
(in der "faulen" Version auch
"(A B)" Formeln
(in der "faulen" Version auch
"(A 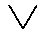 B)"
sowie "(A B)"
sowie "(A  B)".). B)".).
- Ist A eine Formel und x eine Individuenvariable,
so ist "
 x A" eine Formel
(in der "faulen" Version auch
" x A" eine Formel
(in der "faulen" Version auch
"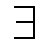 x A") x A")
|
Aus Gründen besserer Lesbarkeit darf man auch Klammerpaare
(sinnvoll) einfügen.
Wieder ist vielleicht interessant, was man nicht machen darf:
Etwa über Relationen oder Operatoren quantifizieren, oder auch über
andere Elemente, etwa natürliche Zahlen, falls
die Grundmenge M nicht N ist---man
hat dann ja nicht einmal Symbole für natürliche Zahlen!
Beweise oder Definitionen werden oft durch
"Induktion über den Term- oder Formelaufbau"
geführt, wir geben Beispiele:
Wir definieren Prädikate var T
(x  var T falls Variable x im Term T vorkommt)
durch Induktion über den Termaufbau:
var T falls Variable x im Term T vorkommt)
durch Induktion über den Termaufbau:
- var ci = Ø und var x = {x},
- var Fj t1 ... tf =
var t1
 ...
...  var tr.
var tr.
Wir definieren Prädikate var A
(x  var A falls x in A vorkommt)
und frei A
(x
var A falls x in A vorkommt)
und frei A
(x  frei A falls x in A frei vorkommt) für Formeln A
durch Induktion über den Formelaufbau:
frei A falls x in A frei vorkommt) für Formeln A
durch Induktion über den Formelaufbau:
- frei A = var A = var t
 var s für Gleichungen s = t,
var s für Gleichungen s = t,
frei A = var A = var t1  ...
...  var tr für weitere Primformeln
Rj t1 ... tr,
var tr für weitere Primformeln
Rj t1 ... tr,
- var (A
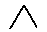 B) = var A
B) = var A  var B,
frei (A
var B,
frei (A 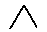 B) = frei A
B) = frei A  frei B,
frei B,
- var
 A = var A,
frei
A = var A,
frei  A = frei A,
A = frei A,
- var
 x A = var A
x A = var A  {x},
frei
{x},
frei  x A = (frei A) \ {x}.
x A = (frei A) \ {x}.
Ist frei A = {x1, x2, ... , xn}
für die Formel A, so schreibt man genauer auch
A(x1, x2, ... , xn) statt A.
Die Generalisierung einer solchen Formel A ist
 x1
x1
 x2 ...
x2 ...
 xn A.
xn A.
Aussagen
Eine Formel, bei der jede Variable gebunden (nichtfrei) ist, nennt man
eine Aussage:
|
Eine Aussage ist eine Formel A mit
frei A = Ø.
|
Grenzen
Wie schon Wittgenstein sagte:
"Wovon man nicht sprechen kann, darüber muß man schweigen"
(zumindest in erster Ordnung!).
Weiter zur Semantik.
Erich Prisner
erstellt im Juni 2000.

![]() = {
= { ![]() ,
,
![]() , (, ),
, (, ), ![]() , = }.
der technische Zeichen umfasst:
, = }.
der technische Zeichen umfasst:
![]() S*
aller endlichen Worte aus dem Alphabet
S*
aller endlichen Worte aus dem Alphabet
![]() S =
S =
![]()
![]() S.
Wir unterscheiden
Terme,
Formeln und
Aussagen,
S.
Wir unterscheiden
Terme,
Formeln und
Aussagen,
![]() var T falls Variable x im Term T vorkommt)
durch Induktion über den Termaufbau:
var T falls Variable x im Term T vorkommt)
durch Induktion über den Termaufbau:
![]() var A falls x in A vorkommt)
und frei A
(x
var A falls x in A vorkommt)
und frei A
(x ![]() frei A falls x in A frei vorkommt) für Formeln A
durch Induktion über den Formelaufbau:
frei A falls x in A frei vorkommt) für Formeln A
durch Induktion über den Formelaufbau:
![]() x1
x1
![]() x2 ...
x2 ...
![]() xn A.
xn A.