
DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000
Rekursionsgleichungen
Inhalt
Bei vielen Anzahlfragen gelten gewisse
Rekursionsgleichungen.
Es werden drei "Methoden" vorgestellt, wie man
sie auflöst, d..h. in geschlossene
Form bringt.
- Raten der Lösung.
- Black-Box Verfahren
für gewisse Rekursionsgleichungen,
ohne Begründung warum es funktionert,
für diejenigen, die das 4-Schritt Verfahren nicht lesen
wollen oder können.
- Ein 4-Schritte Verfahren,
sehr weit anwendbar (obwohl es auch nicht immer funktioniert),
und arbeitet mit
formalen Potenzreihen
Die später in der Analysis benötigte
Partialbruchzerlegung
ist wesentlicher Bestandteil.
Definition:
Für eine Folge (an) ist eine Rekursionsgleichung
eine Gleichung
an = f(an-1,
... ,an-k),
die für beliebiges n 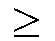 k
gilt und in der nur an, an-1,
... ,an-k,
die Variable n, sowie Konstanten vorkommen. k
gilt und in der nur an, an-1,
... ,an-k,
die Variable n, sowie Konstanten vorkommen.
|
 Für jede gegebenen Anfangswerte a0, a1,
... , ak
ist dann der Rest der Folge eindeutig bestimmt.
Für jede gegebenen Anfangswerte a0, a1,
... , ak
ist dann der Rest der Folge eindeutig bestimmt.
|
Beweis durch vollständige Induktion:
........
Beweis mittels kleinstem Verbrecher
(Wohlordnung):
Angenommen zwei verschiedene Folgen (an)
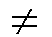 (a'n)
erfüllen die Rekursionsgleichung samt Anfangswerten.
Da die Folgen verschieden sind, gibt es eine kleinste
natürliche Zahl t mit at (a'n)
erfüllen die Rekursionsgleichung samt Anfangswerten.
Da die Folgen verschieden sind, gibt es eine kleinste
natürliche Zahl t mit at 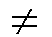 a't, und wegen der gleichen Anfangswerte ist
t > k. Dann ist aber at =
f(at-1,
... ,at-k) =
f(a't-1,
... ,a't-k) =
a't, ein Widerspruch.
a't, und wegen der gleichen Anfangswerte ist
t > k. Dann ist aber at =
f(at-1,
... ,at-k) =
f(a't-1,
... ,a't-k) =
a't, ein Widerspruch.
|
Beispiel 1: an+1 = 3an -
5, a1 = 3.
Die Folgenglieder sind 3, 4, 7, 16, 43, 124, 367, ...
 an = (3n-1+5)/2.
an = (3n-1+5)/2.
|
Beweis durch Vollständige Induktion.
IA: a_1 = (1+5)/2 = 3.
IS: Wir setzen an = (3n-
1+5)/2 für festes n voraus.
Dann ist an+1 = 3an -5
= 3(3n-1+5)/2
- 5 =
(3n + 15 -10)/2 =
(3n + 5)/2.
Diese Formel hätten wir aber auch herleiten können:
Setze bn = an -5/2.
Dann gilt offenbar die einfachere Rekursionsgleichung
bn+1 = an+1 -
5/2 = 3an - 15/2 =
3bn und b1 = 1/2.
Hier ist die Auflösung einfach: bn
= 3n-1/2,
und somit
an = (3n-1
-5)/2.
Doch schon bei einfachsten Rekursionsgleichungen
lässt sich die geschlossene Form nicht mehr raten:
Beispiel 2: Fn+2 = Fn+1 +
Fn, F0 = 0, F1 = 1.
Diese Rekursionsformel bestimmt die sogenannten
Fibonaccizahlen.
 Binet (1843)
wobei
Binet (1843)
wobei 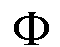 =
(1 + =
(1 + 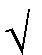 5)/2 5)/2
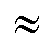 1.61803
der sogenannte "goldene Schnitt" ist.
Beweis: 1.61803
der sogenannte "goldene Schnitt" ist.
Beweis:
|
Erich Prisner
erstellt im Februar 2000.
