
DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000
Binomialkoeffizienten
Aus der Schule kennt jeder die Formeln
|
| |
| | (a+b)3 = a3 + 3a2b + 3ab2 + b3. |
|
| |
|
Wie geht es weiter?
Für zwei natürliche Zahlen
0 £ k £ n
ist der Binomialkoeffizient
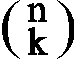 die Anzahl der k-elementigen Teilmengen einer
n-elementigen Menge.
die Anzahl der k-elementigen Teilmengen einer
n-elementigen Menge.
|
Man spricht (und ich schreibe der Einfachheit halber manchmal)
"n über k". Die englische Bezeichnung ist suggestiver:
"n choose k"---es wird also etwas ausgewählt, und zwar
(alle) k-elementigen Teilmengen.
Beispielsweise ist (4 über 2) = 6, denn
{1,2},{1,3},{1,4},{2,3},{2,4},{3,4} sind die zweielementigen
Teilmengen von {1,2,3,4}.
Wie groß ist nun
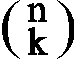 ?
Da jede n-elementige Menge M nur eine 0-elementige
Teilmenge (nämlich Æ)
und nur eine n-elementige
Teilmenge (nämlich M selbst) enthält, ist
(n über 0) = (n über n) = 1 für jedes
n ³0.
?
Da jede n-elementige Menge M nur eine 0-elementige
Teilmenge (nämlich Æ)
und nur eine n-elementige
Teilmenge (nämlich M selbst) enthält, ist
(n über 0) = (n über n) = 1 für jedes
n ³0.
Betrachten wir die Menge {1,2,...,n} wobei 0 < k < n sein soll
(sonst wissen wir ja (n über k) schon).
Eine k-elementige Teilmenge hat "Typ 1", wenn sie "n" enthält,
andernfalls hat sie "Typ 2".
Mit der Summenregel
genügt es, die Anzahlen #Typ1, #Typ2
der k-elementigen Teilmengen von
Typ 1 bzw. von Typ 2 zu bestimmen.
Es gibt eine bijektive Abbildung f von der Menge der
Typ-1-k-elementigen Teilmengen von {1,2,...,n}
auf die Menge der k-1-elementigen Teilmengen von {1,2,...,n-1},
nämlich f(A) := A \ {n}. Also ist #Typ1 =
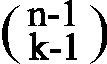 .
.
Es gibt auch eine bijektive Abbildung g von der Menge der
Typ-2-k-elementigen Teilmengen von {1,2,...,n}
auf die Menge der k-elementigen Teilmengen von {1,2,...,n-1},
nämlich g(A) := A. Also ist #Typ2 =
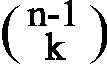 .
.
Somit haben wir
 |
| ( |
|
) |
= |
( |
|
) |
+ |
( |
|
) |
für alle 0 < k < n.
|
|
|
Damit können wir alle Binomialkoeffizienten berechen,
etwa (6 über 3) = (5 über 2) + (5 über 3) =
(4 über 1) + (4 über 2) + (4 über 2) + (4 über 3) =
(4 über 1) + 2(4 über 2) + (4 über 3) =
(3 über 0) + (3 über 1) + 2(3 über 1) + 2(3 über 2) +
(3 über 2) + (3 über 3) =
1 + 3(3 über 1) + 3(3 über 2) + 1 =
1 + 3(2 über 0) + 3(2 über 1) + (3(2 über 1)
+ 3(2 über 2) + 1 =
8+ 6(2 über 1) =
8 + 6(1 über 0) + 6(1 über 1) = 8 + 6 + 6 = 20.
Die Binimialkoeffizienten werden oft im sogenannten
Pascal'schen Dreieck dargestellt.
In Zeile n+1 an Stelle k+1
steht 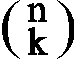 .
Es wird gebildet, indem man an die linke und rechte "Wand" 1en
schreibt (entsprechend unseren Anfangswerten ((n über 0) =
(n über n) = 1) und dann das Innere mittels obiger Rekursionsformel
auffüllt.
.
Es wird gebildet, indem man an die linke und rechte "Wand" 1en
schreibt (entsprechend unseren Anfangswerten ((n über 0) =
(n über n) = 1) und dann das Innere mittels obiger Rekursionsformel
auffüllt.
 Es gibt genau eine Funktion f(n,k) die für alle natürlichen
Zahlen 0 £ k £ n
definiert ist und
Es gibt genau eine Funktion f(n,k) die für alle natürlichen
Zahlen 0 £ k £ n
definiert ist und
die Anfangswerte f(n,0) = f(n,n) = 1 sowie die
Rekursionsgleichung
f(n,k) = f(n-1,k-1)
+ f(n-1,k) für alle 0 < k < n
erfüllt, nämlich
f(n,k) = n!/k!(n-k)!.
Somit gilt
| ( |
|
) |
= |
n!
k! (n-k)!
|
= |
n(n-1)
¼
(n-k+1)
k
(k-1)
¼1
|
. |
|
|
| Beweis: Eindeutigkeit von f wird
ähnlich wie für normale
Rekursionsgleichungen gezeigt.
Dann müssen wir nur noch zeigen, daß obiges f
die Rekursionsgleichung und Anfangswerte erfüllt.
.............
|
Daraus folgt
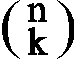 =
=
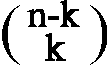 ,
was auch die Symmetrie des Pascal'schen Dreiecks erklärt.
Außerdem steigen die Binomialkoeefizienten in jeder
Zeile erst an, um dann abzufallen, denn wir haben
(n über k+1) - (n über k) =
(n(n-1)...(n-k+1)[n-k - (k+1)]/(k+1)!
,
was auch die Symmetrie des Pascal'schen Dreiecks erklärt.
Außerdem steigen die Binomialkoeefizienten in jeder
Zeile erst an, um dann abzufallen, denn wir haben
(n über k+1) - (n über k) =
(n(n-1)...(n-k+1)[n-k - (k+1)]/(k+1)!
 (n über 0) < (n über 1) < ... <
(n über n/2) > (n über n/2 +1) > ... > (n über n)=1
für gerades n, und
(n über 0) < (n über 1) < ... <
(n über n/2) > (n über n/2 +1) > ... > (n über n)=1
für gerades n, und
(n über 0) < (n über 1) < ... <
(n über (n-1)/2) = (n über (n+1)/2) > ... > (n über n)=1
für ungerades n.
Jetzt weis jeder, wie klein die Chance bei Lotto ist:
1/(49 über 6) = ...
Wie ist die Chance für 5 Richtige und Zusatzzahl?
Zurück zur Ausgangsfrage (a+b)n.
Multiplizieren wir dieses Produkt aus, so sehen wir, daß
nur Terme der Form akbn-k mit
0 £ k £ n
entstehen. Nun fassen wir gleiche Terme zusammen. Wie oft
taucht in der Summe der Term akbn-k auf?
Offenbar so oft, wie wir k mal aus den n Klammerfaktoren "a"
auswählen können. Die Menge der Nummern dieser
ausgewählten Klammern ist eine k-elementige Teilmenge von
{1,2,...,n}, und umgekehrt entspricht jeder solche k-elementiger
Teilmenge eine solche Klammerauswahl, deshalb gibt es genau
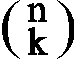 Terme
akbn-k, und wir erhalten:
Terme
akbn-k, und wir erhalten:
 Allgemeine Binomische Formel:
für alle a,b Î R
und jedes n Î N ist
Allgemeine Binomische Formel:
für alle a,b Î R
und jedes n Î N ist
| (a+b)n = |
å
0 £ k
£ n
|
( |
|
) |
akbn
-k. |
|
|
Zum Schluß nochmal zurück zum Pascal'schen Dreieck.
Zuerst addieren wir Elemente der Zeilen.
1+1=2. 1+2+1=4. 1+3+3+1=8. 1+4+6+4+1=16. Sehen Sie wie's weitergeht?
Dann addieren und subtrahieren wir abwechselnd:
1-1=0. 1-2+1=0.
1-3+3-1=0.
1-4+6-4+1=0.
Ist das Zufall?
Nein, wir setzen einfach in der allgemeinen binomischen Formel
a=b=1, bzw. a=1,b=-1, und erhalten:
 |
|
å
0 £
k £ n
|
( |
|
) |
= 2n
und |
å
0 £
k £ n
|
(-1)k |
( |
|
) |
= 2n |
Test
|
Hat eine (nichtleere) Menge mehr Teilmengen mit gerade vielen Elementen
oder mehr Teilmengen mit ungerade vielen Elementen ?
Wieviele Teilmengen hat die Menge {1,2,...10} ?
Wieviel 4-stellige Zahlen (führende Nullen mitgeschrieben)
haben alle Ziffern verschieden?
Im Lotto wurden die Zahlen 4,8,13,16,27,41 gezogen.
Der Abstand zweier gezogenen Zahlen ist hier immer
größer als 1.
Wie wahrscheinlich ist das (auf ganze Prozent gerundet)?
Wollen Sie wissen warum?
|

|
Weiter zu
Rekursionsgleichungen
oder
Anzahlen in unendlichen Mengen.
Erich Prisner
erstellt im Februar 2000.

![]() ?
Da jede n-elementige Menge M nur eine 0-elementige
Teilmenge (nämlich Æ)
und nur eine n-elementige
Teilmenge (nämlich M selbst) enthält, ist
(n über 0) = (n über n) = 1 für jedes
n ³0.
?
Da jede n-elementige Menge M nur eine 0-elementige
Teilmenge (nämlich Æ)
und nur eine n-elementige
Teilmenge (nämlich M selbst) enthält, ist
(n über 0) = (n über n) = 1 für jedes
n ³0.
![]() .
.
![]() .
.
![]() .
Es wird gebildet, indem man an die linke und rechte "Wand" 1en
schreibt (entsprechend unseren Anfangswerten ((n über 0) =
(n über n) = 1) und dann das Innere mittels obiger Rekursionsformel
auffüllt.
.
Es wird gebildet, indem man an die linke und rechte "Wand" 1en
schreibt (entsprechend unseren Anfangswerten ((n über 0) =
(n über n) = 1) und dann das Innere mittels obiger Rekursionsformel
auffüllt.
![]() =
=
![]() ,
was auch die Symmetrie des Pascal'schen Dreiecks erklärt.
Außerdem steigen die Binomialkoeefizienten in jeder
Zeile erst an, um dann abzufallen, denn wir haben
(n über k+1) - (n über k) =
(n(n-1)...(n-k+1)[n-k - (k+1)]/(k+1)!
,
was auch die Symmetrie des Pascal'schen Dreiecks erklärt.
Außerdem steigen die Binomialkoeefizienten in jeder
Zeile erst an, um dann abzufallen, denn wir haben
(n über k+1) - (n über k) =
(n(n-1)...(n-k+1)[n-k - (k+1)]/(k+1)!
![]() (n über 0) < (n über 1) < ... <
(n über n/2) > (n über n/2 +1) > ... > (n über n)=1
für gerades n, und
(n über 0) < (n über 1) < ... <
(n über n/2) > (n über n/2 +1) > ... > (n über n)=1
für gerades n, und
![]() Terme
akbn-k, und wir erhalten:
Terme
akbn-k, und wir erhalten:
![]() Allgemeine Binomische Formel:
für alle a,b Î R
und jedes n Î N ist
Allgemeine Binomische Formel:
für alle a,b Î R
und jedes n Î N ist
