
Erich Prisner
Sommersemester 2000
Dies ist das Internet-Skript zur Vorlesung.
Das Medium "Internet" hat hier vor allem die Vorteile Flexibilität
(es kann noch nachträglich geändert werden) und
einfache Verteilung (kein Papierkrieg).
Außerdem läßt Hypertext die Illusion, es gäbe
eine natürliche lineare Ordnung im Text, gar nicht erst aufkommen.
Insbesondere bei der Darstellung gewisser mathematischer Formeln
gibt es auch Nachteile.
Wie die meisten Skripts erhebt auch dies nicht den Anspruch
Bücher zu ersetzen.
Bücher sind sorgfältiger geschrieben
und meistens auch ausführlicher. Insbesondere warne ich Sie
vor dem Eindruck, Sie könnten die Inhalte der Vorlesung am
Computer sitzend lernen: Zum richtigen Verständnis müssen
Sie selber arbeiten, legen Sie sich also zumindest Papier und Stift bereit!
Mit der Zeit sollten Sie sich vom Bildschirm, und später auch vom
Papier lösen: Sie haben ein Kapitel verstanden, wenn Sie den Inhalt
einem Kommilitonen auf einem Spaziergang erklären können.
Symbole in Unix/Linux/Macintosh/Windows
Sollten Sie in den folgenden beiden Zeilen nicht (nahezu) identische
Symbole sehen, hat Ihr Betriebssystem die Symbol-Fonts nicht.
In dem Fall lesen Sie bitte
HIER weiter.


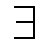




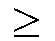

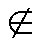


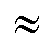

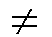
Ø
Ú
Ù
Å
¯
$
Î
"
®
£
³
Í
Ï
È
Ç
»
Æ
¹
Download
 (Version 5.7.)
(Version 5.7.)
---das gepackte Skript
für Windows (enthält z.Zt. etwa 98% des endgültigen Umfangs).
Inhaltsverzeichnis
Inhalt
Diskrete Mathematik beschäftigt sich mit diskreten mathematischen
Strukturen wie etwa
Boolesche Algebren,
Relationen,
(Ordnungsrelationen,,
Äquivalenzrelationen,
Graphen,
gerichtete Graphen (Digraphen),
Funktionen)
Designs,
endliche Geometrien,
Hypergraphen,
lateinische Quadrate,
endliche Körper,
Codes,
oder auch nur
endlichen Teilmengen der Ebene, des Raumes,
oder der Menge der natürlichen Zahlen.
Genauer gesagt handelt die Diskrete Mathematik von Problemen auf
solchen Strukturen und ihren Lösungen.
Außerdem werden in dieser Vorlesung Bereiche aus der
Mengenlehre und Logik behandelt, die eigentlich nicht zum Gebiet der
Diskreten Mathematik gezählt werden.
Da wir also ein "weites Feld" abstecken,
besteht die Gefahr der Verkümmerung der Veranstaltung
zu eine riesigen Definitionensammlung
(siehe Index).
Dieser Gefahr kann ich nur begegnen, indem ich neben die
notwendigerweise formale Beschreibung und Manipulation der Strukturen
soviel wie möglich inhaltliche Mathematik stelle:
Es sollte klar werden, daß Mathematik nicht entsteht
(auch früher nicht!) indem ein Mathematiker mathematische
Strukturen betrachtet und mittels formaler Methoden Sätze ableitet.
Mathematische Sätze entstehen aus klaren, natürlichen
Fragestellungen (oft aus Anwendungsgebieten motiviert),
über die neugierige Menschen so lange
gebrütet haben, bis sie die Antwort nicht nur hatten, sondern
sie sogar weitergeben konnten. Zum Weitergeben der Antwort sowie zum
kritischen Überprüfen ist nun diese formale
Sprechweise unumgänglich.
Obwohl sich die diskrete Mathematik deutlich von der kontinuierlichen
Mathematik abhebt, hat sie viele Verbindungen zu Analysis, (Linearer)
Algebra, Wahrscheinlichkeitstheorie, ... und das in beiden Richtungen.
Begriffe und Methoden der diskreten Mathematik werden dort verwendet
und gebraucht, umgekehrt sind aber auch Methoden der Analysis und Linearen
Algebra für gewisse diskrete Probleme äußerst nützlich.
Viele diese tieferen Verbindungen können wir leider aus
Zeitgründen nicht behandeln.
Scheinkriterien
50% der erreichbaren Punkte bei den Übungsaufgaben
und erfolgreiche Klausur sind zum Erzielen eines Scheines
notwendig. Die Klausur wird in der 12. Semesterwoche
geschrieben, die Wiederholungsklausur in der 14. (letzten)
Semesterwoche.
|
| Teilnehmer | Bestanden | Durchschnittsnote |
| Klausur: |
IMT: 35
Inf: 65 |
30
59 |
2,99
2,85 |
| Wiederholungsklausur |
IMT: 25
Inf: 10 |
15
5 |
3,89
4,4 |
Mitarbeit am Skript
Sie sind herzlich eingeladen, sich am Aufbau und der Pflege des
Skripts zu beteiligen.
Bitte weisen Sie mich auf alle Tippfehler, Unklarheiten, Inhaltsfehler, ...
hin. Auf diese Weise kann das Skript während des Semesters immer besser
werden. Für diejenigen unter Ihnen, die schon Java beherrschen---
einige Java-Applets würden den Spaß, den man mit diesen
Seiten haben kann, sicher erhöhen.
Bisher gingen nützliche Tips von Annett Wenzel, Kerstin Buchholz
und Michael Kühn ein. Vielen Dank.
Vorlesungsplan
Erich Prisner
erstellt im März 2000,
zuletzt geändert am 13.7. 2000.

 (Version 5.7.)
(Version 5.7.)
