Dann hat (X, £ ) die Fixpunkteigenschaft. |

| Eine geordnete Mengen (M,£) hat die Fixpunkteigenschaft, falls jeder Homomorphismus f: M ® M einen Fixpunkt, d.h. ein x Î M mit f(x)=x, hat. |
Die Frage, welche geordneten Mengen diese Fixpunkteigenschaft besitzen ist schwierig (NP-vollständig, Duffus/Goddard), aber für gewisse Klassen geordneter Mengen kann die Eigenschaft nachgewiesen werden:
Dann hat (X, £ ) die Fixpunkteigenschaft. |
Aus obigem Fixpunktsatz folgt, da in vollständigen Verbänden stets 0 £ f(0) gilt,
direkter Beweis |
Übungsaufgabe: Beweisen Sie mit Hilfe des Fixpunktsatzes von Knaster/Tarski Banach's Decomposition Theorem: Zu je zwei Mengen A und B und je zwei Abbildungen f: A ® B, g: B ® A, gibt es eine Partition von A in A1 und A2 und eine Partition von B in B1 und B2 so daß f(A1)=B1 und g(B2)=A2 gilt. Hinweis
Die Frage nach der Fixpunkteigenschaft läßt sich auf ein Cliquenproblem in Graphen zurückführen: Zu gegebener geordneter Menge P = (M,£) konstruieren wir einen Graphen G(P) wie folgt:
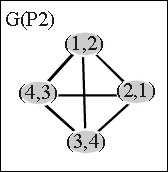
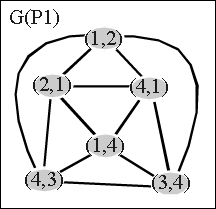 Hier sehen sie zwei geordnete Mengen und die dazugehörigen G(P)s.
Hier sehen sie zwei geordnete Mengen und die dazugehörigen G(P)s.
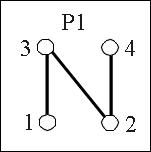
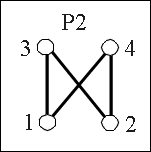
Dann hat f einen Fixpunkt. Beweis |