
DISKRETE MATHEMATIK
Erich Prisner
Sommersemester 2000
Anzahlen
Motivation
-
Wieviele
verschiedene Worte (wie etwa "ABCABB") lassen sich mit
den Buchstaben "A", "A", "B", "B", "B", "C" bilden?
-
|
Auf wieviel
Arten lässt sich ein 7×2 Schachbrett mit 2×1-Dominos
pflastern?
|

|
-
|
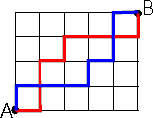
Wieviel
Wege führen von A nach B, wenn es verboten
ist sich nach Süden oder Westen zu bewegen?
Zwei Beispielswege sind gezeigt.
|
|
-
|
Auf wieviel Arten
lassen sich rechteckige Flächen mit diagonal
zweigeteilten Kacheln kacheln, wenn Anstoßkanten
von Kacheln immer verschieden gefärbt sein sollen?
|












|
Alle diese Fragen lassen sich mit etwas Geduld beantworten.
Entsprechenden grösseren Problemen könnte man etwa
lösen indem man Computerprogramme schreibt, die alle
"Konfigurationen" aufzählen.
Es gibt aber auch elegantere Methoden;
einige von ihnen werden wir hier kennenlernen.
Inhalt
Wir werden mit drei ganz einfachen Prinzipien beginnen:
Fast trivial sind
Summenregel
und Produktregel
über die Anzahl von disjunkten Vereinigungen
und kartesischen Produkten.
Das Prinzip der doppelten Abzählung
ist zwar auch sehr einfach, liefert aber manchmal überraschende
Einsichten.
Drittens stellen wir die
Siebformel vor.
Danach werden wir die berühmten
Binomialkoeffizienten streifen,
bevor wir (eventuell) in das wesentlich komplizierte Gebiet
der Rekursionsgleichungen einsteigen.
Was heisst es überhaupt wenn man sagt eine Menge habe
7 Elemente? Dies führt zum Begriff der
Gleichmächtigkeit von Mengen
und zum Begriff
Abzählbarkeit.
Wir werden sehen, daß auch unendliche Mengen
verschieden groß sein können.
Wir starten mit einer Regel, die im Endlichen trivial anmutet
und doch im Unendlichen die Basis für den dortigen Anzahlbegriff ist:
 Eine (endliche) Menge M hat n Elemente, |M| = n, , wenn es eine
bijektive Abbildung
von M auf {1,2,...,n} gibt.
Eine (endliche) Menge M hat n Elemente, |M| = n, , wenn es eine
bijektive Abbildung
von M auf {1,2,...,n} gibt.
 Gleichheitsregel: Gibt es eine bijektive Abbildung von der (endlichen)
Menge A auf B, so ist |A|=|B|.
Gleichheitsregel: Gibt es eine bijektive Abbildung von der (endlichen)
Menge A auf B, so ist |A|=|B|.
 Summenregel:
Sind A und B disjunkte (endliche) Mengen, so ist
| A
Summenregel:
Sind A und B disjunkte (endliche) Mengen, so ist
| A  B | = | A | + | B |. B | = | A | + | B |.
|
Beispiel 1:
Trotz seiner Einfachheit führt dieses Prinzip oft schon zu
Rekursionsgleichungen.
Sei etwa pn die Anzahl der Pflasterungen des n ×2 Schachbretts
mit 2*1-Dominos. Offensichtlich ist p1 = 1, p2 = 2,
p3 = 3, p4 = 5.
Jede solche Pflasterung hat aber ganz links entweder ein vertikales
Domino, oder zwei horizontale Dominos. Jede solche Pflasterung gehört
also genau zu einer der folgenden
beiden Mengen: Entweder zu der Menge Pf1 aller Pflasterungen
der Form
 oder zur Menge Pf2 aller Pflasterungen der Form
oder zur Menge Pf2 aller Pflasterungen der Form
 .
Weil somit die Menge aller Pflasterungen des n ×2 Schachbretts
die disjunkte Vereinigung von Pf1 und Pf2 ist,
gilt nach der Summenregel
pn = | Pf1 | + | Pf2 |.
Da aber ganz offensichtlich | Pf1 | =
pn-1 und
| Pf2 | =
pn-2 gilt,
folgt durch Einsetzen die Rekursionsgleichung
.
Weil somit die Menge aller Pflasterungen des n ×2 Schachbretts
die disjunkte Vereinigung von Pf1 und Pf2 ist,
gilt nach der Summenregel
pn = | Pf1 | + | Pf2 |.
Da aber ganz offensichtlich | Pf1 | =
pn-1 und
| Pf2 | =
pn-2 gilt,
folgt durch Einsetzen die Rekursionsgleichung
Natürlich gelten diese Überlegungen nur falls
n 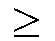 2 ist.
Damit lassen sich pn für
beliebig grosse n automatisch berechnen.
Trotzdem hat diese Gleichung noch einen Nachteil:
Anzahlen von Pflasterungen werden durch
Anzahlen von Pflasterungen ausgedrückt, allerdings zum
Glück (oder leider?) kleineren Ausmaßes.
2 ist.
Damit lassen sich pn für
beliebig grosse n automatisch berechnen.
Trotzdem hat diese Gleichung noch einen Nachteil:
Anzahlen von Pflasterungen werden durch
Anzahlen von Pflasterungen ausgedrückt, allerdings zum
Glück (oder leider?) kleineren Ausmaßes.
Beispiel 2:
Als zweites Beispiel betrachten wir die Anzahl wn,m aller
Wege von A nach B im n ×m Schachbrett.
Zeigen Sie daß wn,m =
wn-1,m +
wn,m-1 gilt.
 Produktregel:
Sind A und B endliche Mengen, so ist
| A ×B | =
| A | |B|.
Produktregel:
Sind A und B endliche Mengen, so ist
| A ×B | =
| A | |B|.
|
Mit der Produktregel folgt (da es eine Bijektion zwischen Mn
und der Menge M{1,2,...,n} aller Abbildungen von {1,2,...,n}
nach M gibt):
 Es gibt kn Abbildungen
von {1,2,...,n} in {1,2,...,k}, suggestiver ausgedrückt:
| {1,2,...,k}{1,2,...,n} | = kn.
Es gibt kn Abbildungen
von {1,2,...,n} in {1,2,...,k}, suggestiver ausgedrückt:
| {1,2,...,k}{1,2,...,n} | = kn.
Spezieller als die Produktregel, folgt folgende Regel aus der Summenregel,
die ich Wahlregel nennen will, da wir die zu zählenden Elemente
mit der Wahl von zwei Parameter erzeugen können.
Wir wählen zuerste den ersten Parameter, und die Entscheidung dieses
Parameters bestimmt die Anzahl der Möglichkeiten, die wir dann
für die Wahl des zweiten Parameters haben. Rekursiv lässt sich
das Prinzip natürlich auf beliebig viele Parameter erweitern.
 Wahlregel:
Die Anzahl einer Relation R
Wahlregel:
Die Anzahl einer Relation R  A × B
sei zu bestimmen. Mit der Abkürzung R(a,.) =
{b A × B
sei zu bestimmen. Mit der Abkürzung R(a,.) =
{b  B/ (a,b) B/ (a,b)  R}
ist R}
ist
| R | = 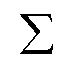 a a A
|R(a,.)|. A
|R(a,.)|.
|
Die Mengen R(a,.) sind i.A. verschieden;
besonders einfach wird die Formel aber, wenn diese Mengen alle
gleich viele Elemente enthalten.
Mit der Wahlregel folgt:
 Es gibt k*(k-1)*(k-2)* ... *(k-n+1) injektive Abbildungen
von {1,2,...,n} in {1,2,...,k}. Speziell gibt es
n! = n*(n-1)* ... *3*2*1 bijektive Abbildungen von {1,2,...,n} in {1,2,...,n}---diese
bij. Abbildungen werden Permutationen genannt,
Es gibt k*(k-1)*(k-2)* ... *(k-n+1) injektive Abbildungen
von {1,2,...,n} in {1,2,...,k}. Speziell gibt es
n! = n*(n-1)* ... *3*2*1 bijektive Abbildungen von {1,2,...,n} in {1,2,...,n}---diese
bij. Abbildungen werden Permutationen genannt,
Oft ist entscheidend, in welcher Reihenfolge man die Wahlen trifft.
Betrachten wir die Anzahl aller Anordnungen der Buchstaben
"A", "B", "C", "D", "E", "F", "G", bei der "A" an erster Stelle,
aber an der letzten Stelle "B" oder "C" stehen muß.
Wählen wir die Buchstaben an den Stellen der Reihe nach,
so wird die Analyse schwierig: Wir haben nur eine Möglichkeit
an der ersten Stelle, 6 Möglichkeit an der zweiten Stelle.
Die Anzahl der Wahlmöglichkeiten an der dritten Stelle
hängt davon ab, ob wir "B" oder "C" an der zweiten Stelle
wählten. Falls ja, dürfen wir "C" oder "B"
an der dritten Stelle nicht wählen, haben also nur
4 Möglichkeiten, sonst 5.
Ganz einfach wird die Analyse, wenn wir zuerst
den Buchstaben an der ersten Stelle (1 Möglichkeit),
dann den Buchstaben an der letzten Stelle
(2 Möglichkeiten), dann den Buchstaben an der
zweiten, dritten, ... sechsten Stelle
(5, 4, 3, 2, 1 Möglichkeiten) wählen.
Es gibt also 1*2*5*4*3*2*1 = 240 solche Anordnungen.
Hier ist ein
weiteres Beispiel dazu.
Prinzip der doppelten Abzählung
Für eine gegebene Matrix berechen wir die Zeilensummen
und die Spaltensummen. Dann ist die Summe aller Spaltensummen
gleich der Summe aller Zeilensummen (gleich der Summe aller Einträge
der Matrix). In der Zeit manuellen Rechnens wurde diese Beobachtung
zur Kontrolle verwendet.
Für einen gegebenen
bipartiten Graphen mit Bipartition
A und B gibt es zwei einfache Möglichkeiten die Zahl der Kanten
zu bestimmen. Einerseits ist sie gleich der Summe der Grade aller Ecken
in A, aber natürlich auch gleich der Summe der Grade aller Ecken
in B.
 Prinzip der doppelten Abzählung:
Sei R
Prinzip der doppelten Abzählung:
Sei R  {a1,a2, ... ,am}
×{b1,b2, ... ,
bn}
eine Relation.
Für jedes 1
{a1,a2, ... ,am}
×{b1,b2, ... ,
bn}
eine Relation.
Für jedes 1  i i  m sei d(ai) die Zahl der bj mit
(ai,bj)
m sei d(ai) die Zahl der bj mit
(ai,bj)  R,
und genauso sei für jedes 1 R,
und genauso sei für jedes 1  j j
 n d(bj)
die Zahl der ai die mit bj in Relation stehen.
Dann gilt n d(bj)
die Zahl der ai die mit bj in Relation stehen.
Dann gilt
|
|
m
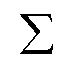
i = 1
|
d(ai) = |
n
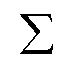
j = 1
|
d(bj) |
|
|
Siebformel
Wieviel Elemente entält die Vereinigung nichtdisjunkter endlicher Mengen?
Zählen wir die Elemente von A und B separat, so haben wir
alle Elemente von A  B gezählt,
aber die Elemente von A
B gezählt,
aber die Elemente von A  B
doppelt. Deshalb gilt | A
B
doppelt. Deshalb gilt | A  B | =
| A | + | B | - | A
B | =
| A | + | B | - | A
 B |.
B |.
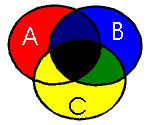
Wie sieht es bei drei Mengen A, B, und C aus?
Überlegen Sie sich wie oben daß gelten muss:
| A  B B
 C | =
| A | + | B | + | C | - | A C | =
| A | + | B | + | C | - | A
 B |
- | A B |
- | A  C | - | B C | - | B
 C | + | A C | + | A  B B
 C |. C |.
|
|
 Siebformel:
Sind A1, A2, ... , An endliche Mengen, so ist
Siebformel:
Sind A1, A2, ... , An endliche Mengen, so ist
|A1  A2 A2
 ... ...  An
| = a1
- a2 +
a3 - ... +
(-1)n-1
an, An
| = a1
- a2 +
a3 - ... +
(-1)n-1
an, |
|
wobei jedes ai
= 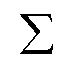 S S  {1,2,...,n}, |S |
= i
|
{1,2,...,n}, |S |
= i
|
 x x  S Ax | ist.
S Ax | ist.
Beweis
|
D.h. wir haben
a1 =
|A1|+
|A2|+ ... +|An
|,
a2 =
|A1  A2|+
|A1
A2|+
|A1  A3|+ ... +
An-1
A3|+ ... +
An-1
 An|,
usw, bis schliesslich
An|,
usw, bis schliesslich
an =
|A1  A2
A2
 ...
...
 An|.
An|.
Noch eine etwas andere Formulierung:
|
| |

1  i
i  n
n
|
Ai|
= |
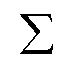

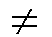 I
I  {1,2, ... ,n}
{1,2, ... ,n}
|
(-1)
|I
|+1
| |

i  I I
|
Ai| |
|
Als Folgerung ergibt sich:
 Die Anzahl der surjektiven Abbildungen von {1,2,...,n} nach {1,2,...,k} ist gleich
Die Anzahl der surjektiven Abbildungen von {1,2,...,n} nach {1,2,...,k} ist gleich
|
Beweis Für jedes j  {1,2,...,k}
sei Aj die Menge aller Abbildungen f von
{1,2,...,n} nach {1,2,...,k}, die j nicht treffen, d.h. mit
f-1({j}) = {1,2,...,k}
sei Aj die Menge aller Abbildungen f von
{1,2,...,n} nach {1,2,...,k}, die j nicht treffen, d.h. mit
f-1({j}) =  .
Aj hat so viele Elemente wie es Abbildungen von
{1,2,...,n} nach {1,2,...,j-1,j+1,...k} gibt, also (k-1)n
nach obigen Bemerkungen.
Für Teilmengen S von {1,2,...,k} ist
| .
Aj hat so viele Elemente wie es Abbildungen von
{1,2,...,n} nach {1,2,...,j-1,j+1,...k} gibt, also (k-1)n
nach obigen Bemerkungen.
Für Teilmengen S von {1,2,...,k} ist
| x x  S Ax| = (k - |S|)n.
Da es genau (k über i) solcher Mengen S gibt,
ist in obiger Formel
ai = (k über i)(k-i)n
für jedes 1
S Ax| = (k - |S|)n.
Da es genau (k über i) solcher Mengen S gibt,
ist in obiger Formel
ai = (k über i)(k-i)n
für jedes 1  i i  k ist.
Die Zahl aller nicht surjektiven Abbildungen ist
|A1 k ist.
Die Zahl aller nicht surjektiven Abbildungen ist
|A1  A2
A2  ...
An| =
a1
-
a2
+ a3
- ... + (-1)n-1
an
von der Geamtzahl kn aller Abbildungen
abgezogen ergibt obige Formel.
...
An| =
a1
-
a2
+ a3
- ... + (-1)n-1
an
von der Geamtzahl kn aller Abbildungen
abgezogen ergibt obige Formel.
|
Test
|
Von den 73 Studenten einer Vorlesung spielen 52 Klavier (!),
25 Violine, 20 Flöte. 17 Studenten beherrschen Klavier und Violine,
12 Klavier und Flöte, 7 Violine und Flöte, aber nur
ein Student beherrscht alle drei Instrumente.
Wieviel Studenten spielen keins dieser drei Instrumente?
Jeder Student besucht genau 3 der 7 angebotenen Vorlesungen.
Diese sieben Vorlesungen haben 73, 20, 20, 11, 4, 4 und 3 Hörer.
Wieviel Studenten gibt es?
|

|
Mathematik ist überall im täglichen Leben,
oder?
Weiter zu
Erich Prisner
File partially translated from
TEX by
T
TH, version 2.53.
erstellt im Februar, geändert im Mai 2000.



 oder zur Menge Pf2 aller Pflasterungen der Form
oder zur Menge Pf2 aller Pflasterungen der Form
 .
Weil somit die Menge aller Pflasterungen des n ×2 Schachbretts
die disjunkte Vereinigung von Pf1 und Pf2 ist,
gilt nach der Summenregel
pn = | Pf1 | + | Pf2 |.
Da aber ganz offensichtlich | Pf1 | =
pn-1 und
| Pf2 | =
pn-2 gilt,
folgt durch Einsetzen die Rekursionsgleichung
.
Weil somit die Menge aller Pflasterungen des n ×2 Schachbretts
die disjunkte Vereinigung von Pf1 und Pf2 ist,
gilt nach der Summenregel
pn = | Pf1 | + | Pf2 |.
Da aber ganz offensichtlich | Pf1 | =
pn-1 und
| Pf2 | =
pn-2 gilt,
folgt durch Einsetzen die Rekursionsgleichung

