Auf dieser Einführungsseite definieren wir Ordnungsrelationen bzw. geordnete Mengen, und stellen einige wichtige Definitionen vor. Endliche Ordnungen werden mittels Hasse-Diagramme dargestellt. Schließlich stellen wir den Satz von Dilworth vor, der eine wichtige und überraschende Beziehung herstellt und als Beispiel und Prototyp für eine Vielzahl ähnlicher Sätze dient.
Auf Folgeseiten werden besonders wichtige Ordnungen behandelt: Lineare Ordnungen und Wohlordnungen und speziellen Wohlordnungen, Ordinalzahlen genannt, sowie Verbände mit den noch spezielleren Booleschen Algebren, die im Endlichen Potenzmengen endlicher Mengen mit der Inklusionsbeziehung versehen sind. Außerdem stellen einige wir Fixpunktsätze vor.
| Definition: Eine reflexive, antisymmetrische und transitive binäre Relation auf einer Menge M wird Ordnungsrelation genannt. Die Menge, zusammen mit der Relation heißt dann eine geordnete Menge. |
Als Relationszeichen bei geordneten Mengen verwendet man meist " £ ". Statt "(a,b) Î £" schreibt man "a £ b". Zwei Elemente a ¹ b sind vergleichbar falls a £ b oder b £ a, und andernfalls unvergleichbar. Eine Kette ist eine Menge paarweise vergleichbarer Elemente, eine Antikette eine Menge paarweise unvergleichbarer Elemente.
|
Sei (M, £ ) eine geordnete Menge
und A Í M.
Ein Element x Î M mit "a Î A: a £ x heisst obere Schranke von A (in (M, £ )). Genauso ist eine untere Schranke ein y Î M mit "a Î A: y £ a. Gibt es ein x Î A (!) mit "a Î A: a £ x, so heißt x das (!) grösste Element von A. Genauso ist das kleinste Element von A (falls existent) definiert. Hat A eine kleinste obere Schranke, so wird es Supremum von A genannt, ebenso wird die größte untere Schranke (falls existent) Infimum von A genannt. |
Ein maximales Element von (M,£)
ist ein x Î M
mit der Eigenschaft, daß aus x £ y
immer x=y folgt. Entsprechend ist ein
minimales Element jedes x Î M
mit (" y Î M :
y £ x ® x=y).
Hat A Í M das Supremum a, (Infimum a')
und ist b Ï A,
so hat A È {b} genau dann ein Supremum (Infimum),
wenn {a,b} ein Supremum (bzw. {a',b} ein Infimum) hat.
Die beiden Suprema (bzw. die beiden Infima)
sind dann gleich
Beweis: s sei das Supremum von {a,b}.
Dann ist s obere Schranke von A È {b}.
Für jede weitere obere Schranke x von
A È {b} ist, wegen der Supremumseigenschaft
von a, a £ x. Also ist x obere Schranke
von {a,b}, und somit s £ x.
Sei umgekehrt t das Supremum von A È {b}.
Da t dann auch obere Schranke von A ist, folgt
a £ t.
Somit ist t obere Schranke von {a,b}.
Jede weitere obere Schranke y von {a,b} ist obere Schranke von
A È {b}, folglich y £ t.
Der Beweis des Infimum-Falles geht analog---vertausche überall
"Infimum" und "Supremum" sowie "£" und
"³".
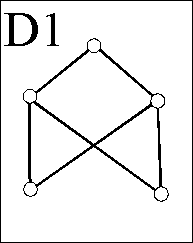
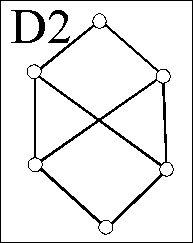
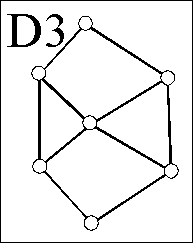
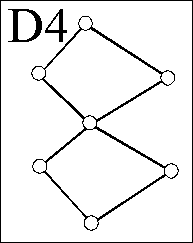
Darstellung durch Hasse-Diagramme
Ordnungsrelationen auf einer endlichen Menge A
lassen sich natürlich als gerichtete Graphen auf A darstellen.
Dieser gerichtete Graph enthält allerdings redundante Information.
Sie kann man folgendermaßen eliminieren:
Zuerst ordnet man die Elemente von A so in der Ebene an, daß
aus a £ b (a ¹ b)
immer folgt, daß
die y-Koordinate des Bildes von a kleiner als die
y-Koordinate des Bildes von b ist
(Wie?).
Damit sind alle gerichteten Kanten von
unten nach oben orientiert, weshalb die Pfeile durch Linien ersetzt werden
können.
Weiterhin ersetzen wir eine Kante von a nach b
wenn es ein c ¹ a,b gibt mit
a £ c £ b
(also ein c "zwischen" a und b), denn dann ergibt sich die
Beziehung a £ b
transitiv aus a £ c £ b.
(Mit anderen Worten: Wir zeichnen eine Kante von x nach y
nur dann wenn y oberer Nachbar von x ist.)
Das so entstehende Bild wird
Hasse-Diagramm
der endlichen geordneten Menge genannt.
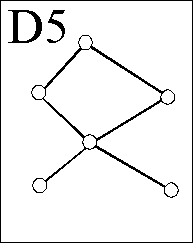
Hier ist ein Beispiel (wobei im Digraphen links alle Schlingen vergessen wurden
und dazugedacht werden sollten):
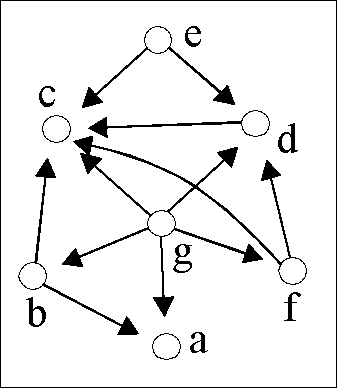
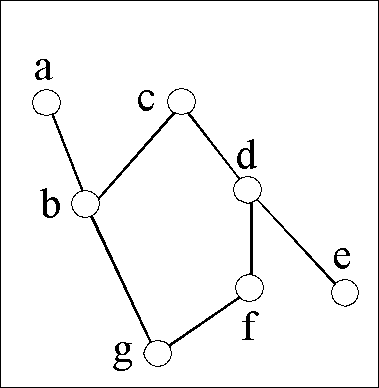
Kartesische Produkte
Das kartesische Produkt von geordneten Mengen
(Xi,£i)
hat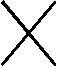 
i Î I
Xi als Grundmenge.
Es gilt (xi) £ (yi)
falls für alle Indizes i gilt
xi £i yi.
Es gibt noch eine zweite Möglichkeit kartesische Produkte
zu ordnen, die sogenannte lexikographische Ordnung.
Dazu muß die Indexmenge I allerdings
wohlgeordnet sein.
Wir definieren es hier nur für I = {1,2,...,n}.
Dann ist (x1,x2,...,xn)
<Lex (y1,y2,...,yn)
falls
es ein 1 £ t £ n
gibt mit
xt <t yt und
xi = yi für alle
1 £ i < t.
Beispiel:
Ideale
Jede Menge M £
P(X) von Mengen ist bzgl.
"Í" geordnet. Wir werden sehen, daß wir so
(bis auf Isomorphie) alle geordneten Mengen erhalten.
Ein Ideal (genauer "lower order ideal")
ist eine Teilmenge A einer geordneten Menge (M,Î)
mit der Eigenschaft,
daß aus x £ a und a Î A
immer schon x Î A folgt. Die primitiven Ideale
sind die Mengen Mx =
{y Î M/y £ x}.
Man kann leicht zeigen:
Jede geordnete Menge (M,£)
ist zur geordneten Menge
({Mx/x Î M},Í) isomorph.
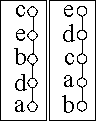Übungsaufgabe:
Es seien zwei lineare Ordnungen L1, L2,
auf {a,b,c,d,e} gegeben, siehe die Hasse Diagramme rechts.
Zeigen Sie, daß der Durchschnitt der Relationen
L1Ç L2
wieder eine Ordnungsrelation ist, und zeichnen Sie das Hasse Diagramm.
b) Ist der Durchschnitt zweier Ordnungsrelationen immer wieder
Ordnungsrelationen?
c) Falls ja, gibt es einen Zusammenhang zwischen den
Dilworth-Zahlen
von R1, R2
und R1Ç R2?
Welches dieser fünf Diagramme
ist kein Hasse Diagramm einer geordneten Menge? Welches von ihnen ist Hasse Diagramm eines Verbandes? |
|